【题目】已知函数![]() 。
。
(1)若f(x)在![]() 上为增函数,求m的取值范围;
上为增函数,求m的取值范围;
(2)若f(x)的值域为R,求m的取值范围。
参考答案:
【答案】(1)![]() ; (2)
; (2)![]() .
.
【解析】
(1)根据复合函数“同增异减”,知t=![]() 为减函数,根据对数的概念,知t=
为减函数,根据对数的概念,知t=![]() >0在(-∞,
>0在(-∞,![]() 上恒成立,分类讨论,进而确定m的取值范围 ;
上恒成立,分类讨论,进而确定m的取值范围 ;
(2)由f(x)的值域为R,得t=![]() 值域为(0,+∞),结合二次函数的性质得到关于m的不等式,解不等式即可.
值域为(0,+∞),结合二次函数的性质得到关于m的不等式,解不等式即可.
由题意y=![]() 可看成由y=
可看成由y=![]() 与t=
与t=![]() 复合而成
复合而成
由于f(x)在(-∞,![]() 上为增函数,根据对数函数的单调性,
上为增函数,根据对数函数的单调性,
所以t=![]() 在(-∞,
在(-∞,![]() 上为减函数,且
上为减函数,且![]() 在(-∞,
在(-∞,![]() 上恒成立
上恒成立
当m=0时,不符合题意;
当m>0时,要符合题意,应满足![]() 且4m-1>0,所以
且4m-1>0,所以![]() <m
<m![]() ;
;
当m<0时,不符题意;
综上,![]() <m
<m![]() ;
;
(2)由f(x)的值域为R,t=![]() 值域为(0,+∞)
值域为(0,+∞)
当m=0时,t=-2x+3,在x<![]() 的值域为(0,+∞),符合题意;
的值域为(0,+∞),符合题意;
当m>0时,要符合题意,应满足![]() 即4-12m
即4-12m![]() ;
;
当m<0时,不符合题意。
综上,![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=lnx﹣mx+m,m∈R.
(1)已知函数f(x)在点(l,f(1))处与x轴相切,求实数m的值;
(2)求函数f(x)的单调区间;
(3)在(1)的结论下,对于任意的0<a<b,证明: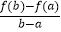 <
< 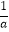 ﹣1.
﹣1. -
科目: 来源: 题型:
查看答案和解析>>【题目】从椭圆
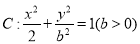 上一点
上一点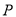 向
向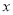 轴作垂线,垂足恰好为椭圆的左焦点
轴作垂线,垂足恰好为椭圆的左焦点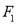 ,
,  是椭圆的右顶点,
是椭圆的右顶点, 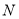 是椭圆的上顶点,且
是椭圆的上顶点,且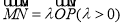 .
.(1)求该椭圆
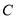 的方程;
的方程;(2)不过原点的直线
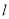 与椭圆
与椭圆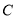 交于
交于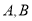 两点,已知
两点,已知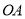 ,直线
,直线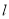 ,
, 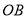 的斜率
的斜率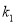 ,
, 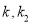 成等比数列,记以
成等比数列,记以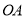 ,
, 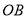 为直径的圆的面积分别为
为直径的圆的面积分别为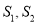 ,求证;
,求证; 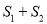 为定值,并求出定值.
为定值,并求出定值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆
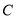 与直线
与直线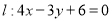 相切于点
相切于点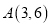 ,且经过点
,且经过点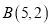 ,求圆
,求圆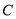 的方程.
的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 是[1,∞]上的增函数.当实数m取最大值时,若存在点Q,使得过Q的直线与曲线y=g(x)围成两个封闭图形,且这两个封闭图形的面积总相等,则点Q的坐标为( )
是[1,∞]上的增函数.当实数m取最大值时,若存在点Q,使得过Q的直线与曲线y=g(x)围成两个封闭图形,且这两个封闭图形的面积总相等,则点Q的坐标为( )
A.(0,﹣3)
B.(0,3)
C.(0,﹣2)
D.(0,2) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知集合
 .
.(1)若
 ,求
,求 的概率;
的概率;(2)若
 ,求
,求 的概率.
的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知λ∈R,函数
 g(x)=x2﹣4x+1+4λ,若关于x的方程f(g(x))=λ有6个解,则λ的取值范围为( )
g(x)=x2﹣4x+1+4λ,若关于x的方程f(g(x))=λ有6个解,则λ的取值范围为( )
A.
B.
C.
D.
相关试题

