【题目】己知在平面直角坐标系![]() 中,圆
中,圆![]() 的参数方程为
的参数方程为 (
(![]() 为参数)以
为参数)以![]() 轴为极轴,
轴为极轴, ![]() 为极点建立极坐标系,在该极坐标系下,圆
为极点建立极坐标系,在该极坐标系下,圆![]() 是以点
是以点![]() 为圆心,且过点
为圆心,且过点![]() 的圆心.
的圆心.
(1)求圆![]() 及圆
及圆![]() 在平而直角坐标系
在平而直角坐标系![]() 下的直角坐标方程;
下的直角坐标方程;
(2)求圆![]() 上任一点
上任一点![]() 与圆
与圆![]() 上任一点之间距离的最小值.
上任一点之间距离的最小值.
参考答案:
【答案】(1)圆M: 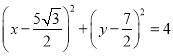 圆N:
圆N: 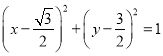 ;(2)
;(2)![]() .
.
【解析】试题分析:
(1)将圆M的参数方程消去参数可得直角坐标方程;把点![]() 化为直角坐标可得圆N的圆心和圆N上的一点,从而可得半径,进而可求得圆的方程。(2)由于两圆相离,故两圆上的两点间的距离的最小值为圆心距减去两半径之和。
化为直角坐标可得圆N的圆心和圆N上的一点,从而可得半径,进而可求得圆的方程。(2)由于两圆相离,故两圆上的两点间的距离的最小值为圆心距减去两半径之和。
试题解析:
(1)将方程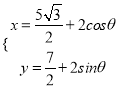 消去参数
消去参数![]() 可得
可得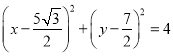 ,
,
所以圆M的方程为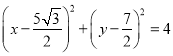 。
。
点![]() 的直角坐标分别为
的直角坐标分别为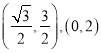 ,
,
所以圆N的圆心为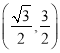 ,半径为
,半径为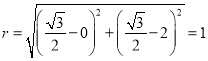 ,
,
故圆N的方程为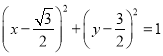 。
。
(2)由(1)得圆M,N的圆心距为
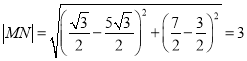 ,
,
所以圆![]() 上任一点
上任一点![]() 与圆
与圆![]() 上任一点之间距离的最小值为
上任一点之间距离的最小值为
![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC的角A、B、C所对的边分别是a、b、c,设向量
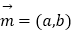 ,
, 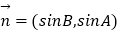 ,
, 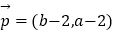 .
.
(1)若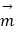 ∥
∥ 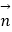 ,求证:△ABC为等腰三角形;
,求证:△ABC为等腰三角形;
(2)若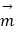 ⊥
⊥ 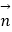 ,边长c=2,角C=
,边长c=2,角C=  ,求△ABC的面积.
,求△ABC的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在三棱锥D-ABC中,已知△BCD是正三角形,AB⊥平面BCD,AB=BC=a,E为BC的中点,F在棱AC上,且AF=3FC
(1)求三棱锥D-ABC的体积
(2)求证:平面DAC⊥平面DEF;
(3)若M为DB中点,N在棱AC上,且CN=
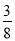 CA,求证:MN∥平面DEF
CA,求证:MN∥平面DEF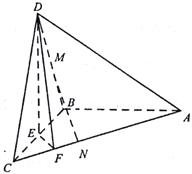
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列{an}的各项均为正数,Sn是数列{an}的前n项和,且4Sn=an2+2an﹣3.
(1)求数列{an}的通项公式;
(2)已知bn=2n , 求Tn=a1b1+a2b2+…+anbn的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】设数列{an}的前n项和为Sn满足2Sn=an+1﹣2n+1+1,n∈N* , 且a1 , a2+5,a3成等差数列.
(1)求a1的值;
(2)求数列{an}的通项公式. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线
 与圆
与圆  且与椭圆
且与椭圆 相交于
相交于 两点.
两点.
(1)若直线
 恰好经过椭圆的左顶点,求弦长
恰好经过椭圆的左顶点,求弦长
(2)设直线
 的斜率分别为
的斜率分别为 ,判断
,判断 是否为定值,并说明理由
是否为定值,并说明理由(3)求
 ,面积的最小值.
,面积的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,小明想将短轴长为2,长轴长为4的一个半椭圆形纸片剪成等腰梯形ABDE,且梯形ABDE内接于半椭圆,DE∥AB,AB为短轴,OC为长半轴
(1)求梯形ABDE上底边DE与高OH长的关系式;
(2)若半椭圆上到H的距离最小的点恰好为C点,求底边DE的取值范围

相关试题

