搜索
【题目】设（x1 ， y1），（x2 ， y2），…，（xn ， yn），是变量x和y的n个样本点，直线l是由这些样本点通过最小二乘法得到的线性回归方程（如图），以下结论中正确的是（ ）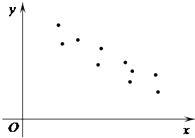 
A.x和y正相关
B.x和y的相关系数为直线l的斜率
C.x和y的相关系数在﹣1到0之间
D.当n为偶数时，分布在l两侧的样本点的个数一定相同
参考答案：
【答案】C
【解析】解：A．由散点图可得，随着x的增加，y逐渐减少，∴x和y是负相关，∴A错误．
B．x和y的相关系数和直线的斜率存在一定的关系，但并不是直线l的斜率，∴B错误．
C．由散点图的分布可以得到x和y的相关系数在﹣1到0之间，∴C正确．
D．当n为偶数时，分布在l两侧的样本点的个数没有直接的关系，∴D错误．
故选：C．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知圆C经过点A（﹣2，0），B（0，2），且圆心C在直线y=x上，又直线l：y=kx+1与圆C相交于P、Q两点．
（1）求圆C的方程；
（2）若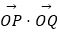
=﹣2，求实数k的值；
（3）过点（0，4）作动直线m交圆C于E，F两点．试问：在以EF为直径的所有圆中，是否存在这样的圆P，使得圆P经过点M（2，0）？若存在，求出圆P的方程；若不存在，请说明理由． -
科目： 来源： 题型：
查看答案和解析>>【题目】已知
为等差数列，前n项和为
，
是首项为2的等比数列，且公比大于0，
，
，
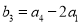．（1）求
和的通项公式；（2）求数列
的前n项和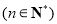
． -
科目： 来源： 题型：
查看答案和解析>>【题目】为了丰富退休生活，老王坚持每天健步走，并用计步器记录每天健步走的步数.他从某月中随机抽取20天的健步走步数（老王每天健步走的步数都在
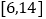之间，单位：千步），绘制出频率分布直方图（不完整）如图所示.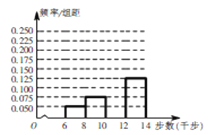
（1）完成频率分布直方图，并估计该月老王每天健步走的平均步数(每组数据可用区间中点值代替；
（2）某健康组织对健步走步数的评价标准如下表:
每天步数分组(千步)
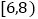
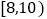
评价级别
及格
良好
优秀
现从这20天中评价级别是“及格”或“良好”的天数里随机抽取2天，求这2天的健步走结果属于同一评价级别的概率.
-
科目： 来源： 题型：
查看答案和解析>>【题目】设函数
。（1）若曲线
在点
处的切线与直线
垂直，求
的单调递减区间和极小值（其中
为自然对数的底数）；（2）若对任意
恒成立，求
的取值范围。 -
科目： 来源： 题型：
查看答案和解析>>【题目】某中学高三年级从甲、乙两个班级各选出7名学生参加数学竞赛，他们取得的成绩（满分100分）的茎叶图如图，其中甲班学生的平均分是85，乙班学生成绩的中位数是83，则x+y的值为 ．
-
科目： 来源： 题型：
查看答案和解析>>【题目】从某居民区随机抽取10个家庭，获得第i个家庭的月收入xi（单位：千元）与月储蓄yi（单位：千元）的数据资料，算得
=80， 
=20， yi=184， 
=720．
（1）求家庭的月储蓄y对月收入x的线性回归方程y=bx+a；
（2）判断变量x与y之间是正相关还是负相关；
（3）若该居民区某家庭月收入为7千元，预测该家庭的月储蓄．
附：线性回归方程y=bx+a中，b=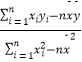
，a= 
﹣b 
，其中 ， 为样本平均值．
相关试题
