[题目]给出如下四个命题:①若“p且为假命题.则p.q均为假命题,②命题“若a>b.则的否命题为“若a≤b.则 ,③“x∈R.的否定是“ ,④在△ABC中.“A>B 是“ 的充要条件,其中正确的命题的个数是( )A.1B.2C.3D.4 题目和参考答案——青夏教育精英家教网—

精英家教网 > 高中数学 > 题目详情

【题目】给出如下四个命题：①若“p且”为假命题，则p、q均为假命题；②命题“若a>b，则”的否命题为“若a≤b，则”；③“x∈R，的否定是“”；④在△ABC中，“A>B”是“”的充要条件；其中正确的命题的个数是（）

A.1B.2C.3D.4

【答案】C

【解析】

根据含有逻辑联结词命题真假性的知识，判断①的正确性.根据否命题的知识，判断②的正确性.根据特称命题的否定的知识，判断③的正确性.根据充要条件的知识，判断④的正确性.

对于①，由于“且”为假命题，所以，中至少有一个假命题，故①错误.

对于②，否命题否定条件和结论，故②正确.

对于③，根据特称命题的否定是全称命题的知识可知，③正确.

对于④，由正弦定理得，所以“”是“”的充要条件，故④正确.

综上所述，正确的命题个数是个.

故选：C

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

【题目】已知抛物线过点，该抛物线的准线与椭圆:相切，且椭圆的离心率为，点为椭圆的右焦点.

（1）求椭圆的标准方程；

（2）过点的直线与椭圆交于两点，为平面上一定点，且满足，求直线的方程.

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】海面上漂浮着、、、、、、七个岛屿，岛与岛之间都没有桥连接，小昊住在岛，小皓住在岛.现政府计划在这七个岛之间建造座桥（每两个岛之间至多建造一座桥）.若，则桥建完后，小吴和小皓可以往来的概率为______；若，则桥建完后，小昊和小皓可以往来的概率为______.

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】某同学理科成绩优异，今年参加了数学，物理，化学，生物4门学科竞赛．已知该同学数学获一等奖的概率为，物理，化学，生物获一等奖的概率都是，且四门学科是否获一等奖相互独立．

（1）求该同学至多有一门学科获得一等奖的概率；

（2）用随机变量表示该同学获得一等奖的总数，求的概率分布和数学期望．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】如图，在四棱柱中，底面为菱形，.

（1）证明：平面平面；

（2）若，是等边三角形，求二面角的余弦值.

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】如图,已知长方形中,,为的中点. 将沿折起,使得平面平面.

(1)求证: .

(2)点是线段上的一动点,当二面角大小为时,试确定点的位置.

查看答案和解析>>

科目：高中数学 来源： 题型：

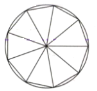
【题目】刘徽(约公元225年-295年)，魏晋期间伟大的数学家，中国古典数学理论的奠基人之一他在割圆术中提出的，“割之弥细，所失弥少，割之又割，以至于不可割，则与圆周合体而无所失矣”，这可视为中国古代极限观念的佳作，割圆术的核心思想是将一个圆的内接正n边形等分成n个等腰三角形(如图所示)，当n变得很大时，这n个等腰三角形的面积之和近似等于圆的面积，运用割圆术的思想，得到的近似值为（）