【题目】已知 ![]() .
.
(Ⅰ)对一切 ![]() 恒成立,求实数
恒成立,求实数 ![]() 的取值范围;
的取值范围;
(Ⅱ)证明:对一切 ![]() ,都有
,都有 ![]() 成立.
成立.
参考答案:
【答案】解:(I) ![]() ,则
,则 ![]() ,
,
设 ![]() ,则
,则 ![]() ,
,![]() 单调递减,②
单调递减,② ![]() 单调递增,
单调递增,
所以 ![]() ,对一切
,对一切 ![]() 恒成立,所以
恒成立,所以 ![]() ;
;
(Ⅱ)问题等价于证明 ![]() ,
,
由(1)可知 ![]() 的最小值是
的最小值是 ![]() ,当且仅当
,当且仅当 ![]() 时取到,
时取到,
设 ![]() ,则
,则 ![]() ,易知
,易知![]() ,当且仅当
,当且仅当 ![]() 时取到,
时取到,
从而对一切 ![]() ,都有
,都有 ![]() 成立
成立
【解析】本题主要考查函数的单调性、最值问题,以及导数的应用和不等式的证明问题。(1)把恒成立的问题要利用转化的思想进行等价转化,把不等式2 f ( x ) ≥ g ( x ) 恒成立的问题转化为a ≤ 2 ln x + x + 3 /x恒成立的问题,进而利用导数求解最小值即可求出a的取值范围。(2)要证明的不等式问题要转化为证明 x ln x > x/ e x 2 /e的问题,根据函数的单调性进行求解即可。
【考点精析】本题主要考查了函数的最大(小)值与导数的相关知识点,需要掌握求函数![]() 在
在![]() 上的最大值与最小值的步骤:(1)求函数
上的最大值与最小值的步骤:(1)求函数![]() 在
在![]() 内的极值;(2)将函数
内的极值;(2)将函数![]() 的各极值与端点处的函数值
的各极值与端点处的函数值![]() ,
,![]() 比较,其中最大的是一个最大值,最小的是最小值才能正确解答此题.
比较,其中最大的是一个最大值,最小的是最小值才能正确解答此题.
-
科目: 来源: 题型:
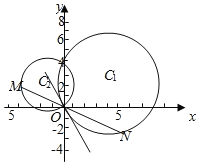
查看答案和解析>>【题目】已知圆
 与y轴交于O,A两点,圆C2过O,A两点,且直线C2O与圆C1相切;
与y轴交于O,A两点,圆C2过O,A两点,且直线C2O与圆C1相切;(1)求圆C2的方程;
(2)若圆C2上一动点M,直线MO与圆C1的另一交点为N,在平面内是否存在定点P使得PM=PN始终成立,若存在求出定点坐标,若不存在,说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某保险公司有一款保险产品的历史收益率(收益率=利润÷保费收入)的频率分布直方图如图所示:
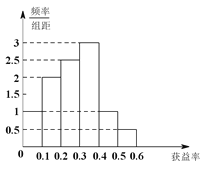
(Ⅰ)试估计平均收益率;
(Ⅱ)根据经验,若每份保单的保费在20元的基础上每增加
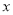 元,对应的销量
元,对应的销量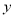 (万份)与
(万份)与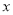 (元)有较强线性相关关系,从历史销售记录中抽样得到如下5组
(元)有较强线性相关关系,从历史销售记录中抽样得到如下5组 与
与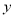 的对应数据:
的对应数据:
据此计算出的回归方程为
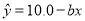 .
.(i)求参数
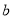 的估计值;
的估计值;(ii)若把回归方程
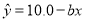 当作
当作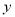 与
与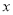 的线性关系,用(Ⅰ)中求出的平均收益率估计此产品的收益率,每份保单的保费定为多少元时此产品可获得最大收益,并求出该最大收益.
的线性关系,用(Ⅰ)中求出的平均收益率估计此产品的收益率,每份保单的保费定为多少元时此产品可获得最大收益,并求出该最大收益. -
科目: 来源: 题型:
查看答案和解析>>【题目】(本小题满分12分)一个盒子里装有三张卡片,分别标记有数字
 ,
, ,
, ,这三张卡片除标记的数字外完全相同。随机有放回地抽取
,这三张卡片除标记的数字外完全相同。随机有放回地抽取 次,每次抽取
次,每次抽取 张,将抽取的卡片上的数字依次记为
张,将抽取的卡片上的数字依次记为 ,
, ,
, .
.(Ⅰ)求“抽取的卡片上的数字满足
 ”的概率;
”的概率;(Ⅱ)求“抽取的卡片上的数字
 ,
, ,
, 不完全相同”的概率.
不完全相同”的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】设椭圆
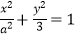 (
( 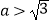 )的右焦点为F,右顶点为A,已知
)的右焦点为F,右顶点为A,已知 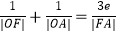 ,其中O 为原点, e为椭圆的离心率.
,其中O 为原点, e为椭圆的离心率.
(Ⅰ)求椭圆的方程;
(Ⅱ)设过点A的直线l与椭圆交于点B(B不在x轴上),垂直于l的直线与l交于点M,与y轴交于点H,若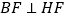 ,且
,且 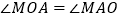 ,求直线的l斜率.
,求直线的l斜率. -
科目: 来源: 题型:
查看答案和解析>>【题目】某大学艺术专业400名学生参加某次测评,根据男女学生人数比例,使用分层抽样的方法从中随机抽取了100名学生,记录他们的分数,将数据分成7组:
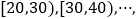
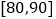 ,并整理得到如下频率分布直方图:
,并整理得到如下频率分布直方图: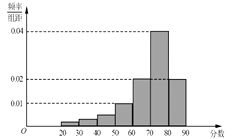
(Ⅰ)从总体的400名学生中随机抽取一人,估计其分数小于70的概率;
(Ⅱ)已知样本中分数小于40的学生有5人,试估计总体中分数在区间[40,50)内的人数;
(Ⅲ)已知样本中有一半男生的分数不小于70,且样本中分数不小于70的男女生人数相等.试估计总体中男生和女生人数的比例. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,
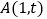 ,
, ,
,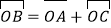 (O是坐标原点),其中
(O是坐标原点),其中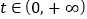 。
。(1)求B点坐标;
(2)求四边形OABC在第一象限部分面积
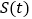 .
.
相关试题

