【题目】某大学艺术专业400名学生参加某次测评,根据男女学生人数比例,使用分层抽样的方法从中随机抽取了100名学生,记录他们的分数,将数据分成7组: ![]()
![]() ,并整理得到如下频率分布直方图:
,并整理得到如下频率分布直方图: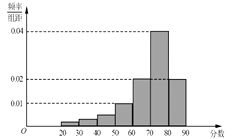
(Ⅰ)从总体的400名学生中随机抽取一人,估计其分数小于70的概率;
(Ⅱ)已知样本中分数小于40的学生有5人,试估计总体中分数在区间[40,50)内的人数;
(Ⅲ)已知样本中有一半男生的分数不小于70,且样本中分数不小于70的男女生人数相等.试估计总体中男生和女生人数的比例.
参考答案:
【答案】解:(I)由频率分布直方图知,
分数在 ![]() 的频率为
的频率为 ![]() ,
,
分数在 ![]() 的频率为
的频率为 ![]() ,
,
则分数小于70的频率为 ![]() ,
,
故从总体的400名学生中随机抽取一人,估计其分数小于70的概率为 ![]() .
.
(Ⅱ)由频率分布直方图知,
样本中分数在区间 ![]() 的人数为
的人数为 ![]() (人),
(人),
已知样本中分数小于40的学生有5人,
所以样本中分数在区间 ![]() 内的人数为
内的人数为 ![]() (人),
(人),
设总体中分数在区间 ![]() 内的人数为
内的人数为 ![]() ,
,
则 ![]() ,得
,得 ![]() ,
,
所以总体中分数在区间 ![]() 内的人数为20人.
内的人数为20人.
(Ⅲ)由频率分布直方图知,
分数不小于70的人数为 ![]() (人),
(人),
已知分数不小于70的男女生人数相等,
故分数不小于70分的男生人数为30人,
又因为样本中有一半男生的分数不小于70,
故男生的频率为: ![]() ,
,
即女生的频率为: ![]() ,
,
即总体中男生和女生人数的比例约为: ![]()
【解析】本题主要考查频率分布直方图,以及用样本估计总体。(1)主要根据频率分布直方图中的频率=组距×高,可得分数小于70的概率。(2)先计算样本中分数在区间【50,90】之间的人数,分别计算【40,50】之间的,小于40的人数,进而求出总体中【40,50】之间的人数。(3)已知样本中有一半男生的分数不小于70,且样本中分数不小于70的男女生人数相等,根据频率分布直方图即可求出答案。
【考点精析】根据题目的已知条件,利用频率分布直方图和用样本的频率分布估计总体分布的相关知识可以得到问题的答案,需要掌握频率分布表和频率分布直方图,是对相同数据的两种不同表达方式.用紧凑的表格改变数据的排列方式和构成形式,可展示数据的分布情况.通过作图既可以从数据中提取信息,又可以利用图形传递信息;样本数据的频率分布表和频率分布直方图,是通过各小组数据在样本容量中所占比例大小来表示数据的分布规律,它可以让我们更清楚的看到整个样本数据的频率分布情况,并由此估计总体的分布情况.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(本小题满分12分)一个盒子里装有三张卡片,分别标记有数字
 ,
, ,
, ,这三张卡片除标记的数字外完全相同。随机有放回地抽取
,这三张卡片除标记的数字外完全相同。随机有放回地抽取 次,每次抽取
次,每次抽取 张,将抽取的卡片上的数字依次记为
张,将抽取的卡片上的数字依次记为 ,
, ,
, .
.(Ⅰ)求“抽取的卡片上的数字满足
 ”的概率;
”的概率;(Ⅱ)求“抽取的卡片上的数字
 ,
, ,
, 不完全相同”的概率.
不完全相同”的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 .
.
(Ⅰ)对一切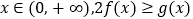 恒成立,求实数
恒成立,求实数  的取值范围;
的取值范围;
(Ⅱ)证明:对一切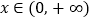 ,都有
,都有 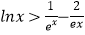 成立.
成立. -
科目: 来源: 题型:
查看答案和解析>>【题目】设椭圆
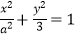 (
( 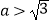 )的右焦点为F,右顶点为A,已知
)的右焦点为F,右顶点为A,已知 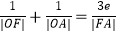 ,其中O 为原点, e为椭圆的离心率.
,其中O 为原点, e为椭圆的离心率.
(Ⅰ)求椭圆的方程;
(Ⅱ)设过点A的直线l与椭圆交于点B(B不在x轴上),垂直于l的直线与l交于点M,与y轴交于点H,若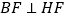 ,且
,且 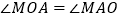 ,求直线的l斜率.
,求直线的l斜率. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,
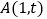 ,
, ,
,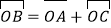 (O是坐标原点),其中
(O是坐标原点),其中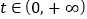 。
。(1)求B点坐标;
(2)求四边形OABC在第一象限部分面积
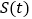 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】设函数
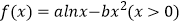 ,若函数
,若函数 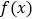 在x=1处与直线
在x=1处与直线 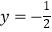 相切.
相切.
(Ⅰ)求实数a,b的值;
(Ⅱ)求函数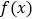 在
在 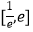 上的最大值.
上的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某旅游爱好者计划从3个亚洲国家
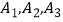 和3个欧洲国家
和3个欧洲国家 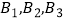 中选择2个国家去旅游.
中选择2个国家去旅游.
(Ⅰ)若从这6个国家中任选2个,求这2个国家都是亚洲国家的概率;
(Ⅱ)若从亚洲国家和欧洲国家中各任选1个,求这2个国家包括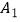 但不包括
但不包括 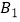 的概率.
的概率.
相关试题

