【题目】已知椭圆![]() 和直线
和直线![]() :
: ![]() ,椭圆的离心率
,椭圆的离心率![]() ,坐标原点到直线
,坐标原点到直线![]() 的距离为
的距离为![]() .
.
(Ⅰ)求椭圆的方程;
(Ⅱ)已知定点![]() ,若直线
,若直线![]() 过点
过点![]() 且与椭圆相交于
且与椭圆相交于![]() 两点,试判断是否存在直线
两点,试判断是否存在直线![]() ,使以
,使以![]() 为直径的圆过点
为直径的圆过点![]() ?若存在,求出直线
?若存在,求出直线![]() 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
参考答案:
【答案】(I)![]() ;(II)
;(II)![]() 或
或![]() .
.
【解析】试题分析:(Ⅰ)根据椭圆中的![]() ,以及
,以及![]() ,和点到直线的距离公式计算求得
,和点到直线的距离公式计算求得![]() ;(Ⅱ)分斜率不存在和斜率存在两种情况讨论,当斜率存在时,设直线为
;(Ⅱ)分斜率不存在和斜率存在两种情况讨论,当斜率存在时,设直线为![]() 与椭圆方程联立,利用根与系数的关系计算
与椭圆方程联立,利用根与系数的关系计算![]() ,从而求得斜率
,从而求得斜率![]() 和直线方程.
和直线方程.
试题解析:(Ⅰ)由直线![]() ,∴
,∴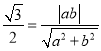 ,即
,即![]() ——①
——①
又由![]() ,得
,得![]() ,即
,即![]() ,又∵
,又∵![]() ,∴
,∴![]() ——②
——②
将②代入①得,即![]() ,∴
,∴![]() ,
, ![]() ,
, ![]() ,
,
∴所求椭圆方程是![]() ;
;
(Ⅱ)①当直线![]() 的斜率不存在时,直线
的斜率不存在时,直线![]() 方程为
方程为![]() ,
,
则直线![]() 与椭圆的交点为
与椭圆的交点为![]() ,又∵
,又∵![]() ,
,
∴![]() ,即以
,即以![]() 为直径的圆过点
为直径的圆过点![]() ;
;
②当直线![]() 的斜率存在时,设直线
的斜率存在时,设直线![]() 方程为
方程为![]() ,
, ![]() ,
, ![]() ,
,
由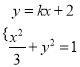 ,得
,得![]() ,
,
由![]() ,得
,得![]() 或
或![]() ,
,
∴![]() ,
, ![]() ,
,
∴![]()
∵以![]() 为直径的圆过点
为直径的圆过点![]() ,∴
,∴![]() ,即
,即![]() ,
,
由![]() ,
, ![]() ,
,
得![]() ,∴
,∴![]() ,
,
∴![]() ,解得
,解得![]() ,即
,即![]() ;
;
综上所述,当以![]() 为直径的圆过定点
为直径的圆过定点![]() 时,直线
时,直线![]() 的方程为
的方程为![]() 或
或![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知等差数列
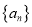 前5项和为50,
前5项和为50, 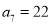 ,数列
,数列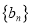 的前
的前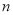 项和为
项和为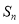 ,
, 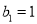 ,
, 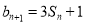 .
.(Ⅰ)求数列
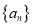 ,
, 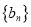 的通项公式;
的通项公式;(Ⅱ)若数列
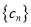 满足
满足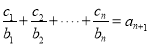 ,
, 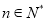 ,求
,求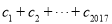 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列{an}的前n项和Sn满足:Sn=
 (an﹣1)(a为常数,且a≠0,a≠1);
(an﹣1)(a为常数,且a≠0,a≠1);
(1)求{an}的通项公式;
(2)设bn= +1,若数列{bn}为等比数列,求a的值;
+1,若数列{bn}为等比数列,求a的值;
(3)若数列{bn}是(2)中的等比数列,数列cn=(n﹣1)bn , 求数列{cn}的前n项和Tn . -
科目: 来源: 题型:
查看答案和解析>>【题目】设数列{an}的前n项和为Sn , 若对任意的正整数n,总存在正整数m,使得Sn=am , 则称{an}是“H数列”.
(1)若数列{an}的前n项和为Sn=2n(n∈N*),证明:{an}是“H数列”;
(2)设{an}是等差数列,其首项a1=1,公差d<0,若{an}是“H数列”,求d的值;
(3)证明:对任意的等差数列{an},总存在两个“H数列”{bn}和{cn},使得an=bn+cn(n∈N*)成立. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆C:x2+y2﹣2x﹣2ay+a2﹣24=0(a∈R)的圆心在直线2x﹣y=0上.
(1)求实数a的值;
(2)求圆C与直线l:(2m+1)x+(m+1)y﹣7m﹣4=0(m∈R)相交弦长的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】为了调查某高中学生每天的睡眠时间,现随机对20名男生和20名女生进行问卷调查,结果如下:
女生:睡眠时间(小时)
[4,5)
[5,6)
[6,7)
[7,8)
[8,9]
人数
2
4
8
4
2
男生:
睡眠时间(小时)
[4,5)
[5,6)
[6,7)
[7,8)
[8,9]
人数
1
5
6
5
3
(1)现把睡眠时间不足5小时的定义为“严重睡眠不足”,从睡眠时间不足6小时的女生中随机抽取2人,求此2人中恰有一人为“严重睡眠不足”的概率;
(2)完成下面2×2列联表,并回答是否有90%的把握认为“睡眠时间与性别有关”?睡眠时间少于7小时
睡眠时间不少于7小时
合计
男生
女生
合计
P(K2≥k)
0.15
0.10
0.05
0.025
0.010
0.005
0.001
k
2.072
2.706
3.841
5.024
6.635
7.879
10.828
(
 ,其中n=a+b+c+d)
,其中n=a+b+c+d) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)的定义域为(﹣∞,0)∪(0,+∞),f(x)是奇函数,且当x>0时,f(x)=x2﹣x+a,若函数g(x)=f(x)﹣x的零点恰有两个,则实数a的取值范围是( )
A.a<0
B.a≤0
C.a≤1
D.a≤0或a=1
相关试题

