
【题目】在“挑战不可能”的电视节目上,甲、乙、丙三个人组成的解密团队参加一项解密挑战活动,规则是由密码专家给出题目,然后由![]() 个人依次出场解密,每人限定时间是
个人依次出场解密,每人限定时间是![]() 分钟内,否则派下一个人.
分钟内,否则派下一个人.![]() 个人中只要有一人解密正确,则认为该团队挑战成功,否则挑战失败.根据甲以往解密测试情况,抽取了甲
个人中只要有一人解密正确,则认为该团队挑战成功,否则挑战失败.根据甲以往解密测试情况,抽取了甲![]() 次的测试记录,绘制了如下的频率分布直方图.
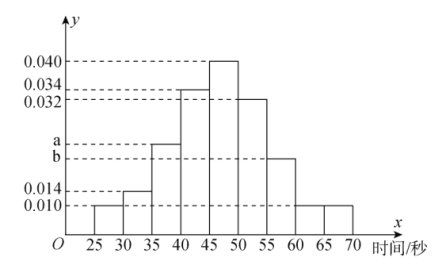
次的测试记录,绘制了如下的频率分布直方图.
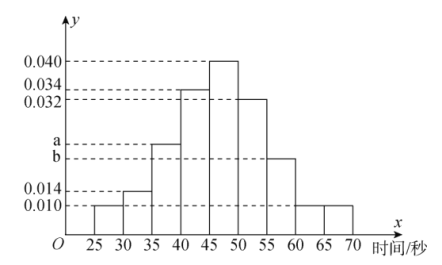
(1)若甲解密成功所需时间的中位数为![]() ,求
,求![]() 、
、![]() 的值,并求出甲在
的值,并求出甲在![]() 分钟内解密成功的频率;
分钟内解密成功的频率;
(2)在“挑战不可能”节目上由于来自各方及自身的心理压力,甲,乙,丙解密成功的概率分别为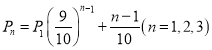 ,其中
,其中![]() 表示第
表示第![]() 个出场选手解密成功的概率,并且
个出场选手解密成功的概率,并且![]() 定义为甲抽样中解密成功的频率代替,各人是否解密成功相互独立.
定义为甲抽样中解密成功的频率代替,各人是否解密成功相互独立.
①求该团队挑战成功的概率;
②该团队以![]() 从小到大的顺序按排甲、乙、丙三个人上场解密,求团队挑战成功所需派出的人员数目
从小到大的顺序按排甲、乙、丙三个人上场解密,求团队挑战成功所需派出的人员数目![]() 的分布列与数学期望.
的分布列与数学期望.
【答案】(1)![]() ,
,![]() ,甲在
,甲在![]() 分钟内解密成功的频率
分钟内解密成功的频率![]() ;(2)①
;(2)①![]() ;②详见解析,
;②详见解析,![]() .
.
【解析】
(1)根据中位数左右两边的矩形面积之和均为![]() 可求得
可求得![]() 、
、![]() 的值,并根据频率分布直方图求得甲在
的值,并根据频率分布直方图求得甲在![]() 分钟内解密成功的频率;
分钟内解密成功的频率;
(2)①由(1)得出![]() ,求出
,求出![]() 、
、![]() 的值,由此得出该团队挑战成功的概率为
的值,由此得出该团队挑战成功的概率为![]() ;
;
②由题意可得出随机变量![]() 的可能取值有
的可能取值有![]() 、
、![]() 、
、![]() ,利用独立事件的概率乘法公式计算出随机变量
,利用独立事件的概率乘法公式计算出随机变量![]() 在不同取值下的概率,据此可得出随机变量
在不同取值下的概率,据此可得出随机变量![]() 的分布列,结合期望公式可计算出
的分布列,结合期望公式可计算出![]() 的数学期望值.
的数学期望值.
(1)甲解密成功所需时间的中位数为![]() ,
,
![]() ,解得
,解得![]() ,
,
![]() ,解得
,解得![]() ,
,
由频率分布直方图知,甲在![]() 分钟内解密成功的频率是
分钟内解密成功的频率是![]() ;
;
(2)①由题意及(1)可知第一个出场选手解密成功的概率为![]() ,
,
第二个出场选手解密成功的概率为![]() ,
,
第三个出场选手解密成功的概率为![]() ,
,
所以该团队挑战成功的概率为![]() ;
;
②由①可知按![]() 从小到大的顺序的概率分别
从小到大的顺序的概率分别![]() 、
、![]() 、
、![]() ,
,
根据题意知![]() 的取值为
的取值为![]() 、
、![]() 、
、![]() ,
,
则![]() ,
,![]() ,
,![]() ,
,
所以所需派出的人员数目![]() 的分布列为:
的分布列为:
|
|
|
|
|
|
|
|
因此,![]() .
.


科目:高中数学 来源: 题型:
【题目】一旅游区有两个新建项目![]() 、
、![]() .
.![]() 项目的一期投资额
项目的一期投资额![]() 与利润
与利润![]() 近似满足
近似满足![]() .
.![]() 项目的一期投资额
项目的一期投资额![]() 与利润
与利润![]() 的关系如散点图所示,其中
的关系如散点图所示,其中![]()
![]() ,
,![]() ,
,![]() .一商家欲向这两个项目一期随机投资,其中投资
.一商家欲向这两个项目一期随机投资,其中投资![]() 项目不超过10(本题未注明金额单位的,单位均为百万元).投资
项目不超过10(本题未注明金额单位的,单位均为百万元).投资![]() 、
、![]() 相互独立.
相互独立.
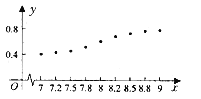
(1)用最小二乘法求![]() 与
与![]() 的回归直线方程;
的回归直线方程;
(2)商家投资![]() 项目的概率是0.4,投资
项目的概率是0.4,投资![]() 项目的概率是0.6.设商家这次投资获得的利润最大值为
项目的概率是0.6.设商家这次投资获得的利润最大值为![]() ,利用(1)的结果,求
,利用(1)的结果,求![]() .
.
附参考公式: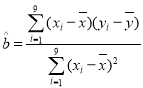 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了调查“双11”消费活动情况,某校统计小组分别走访了![]() 、
、![]() 两个小区各20户家庭,他们当日的消费额按
两个小区各20户家庭,他们当日的消费额按![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分组,分别用频率分布直方图与茎叶图统计如下(单位:元):
分组,分别用频率分布直方图与茎叶图统计如下(单位:元):
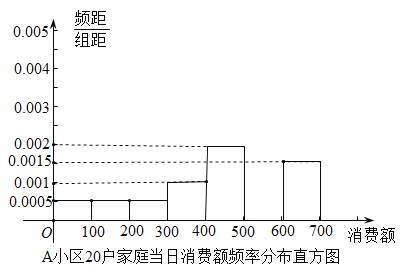
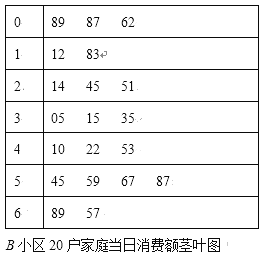
(1)分别计算两个小区这20户家庭当日消费额在![]() 的频率,并补全频率分布直方图;
的频率,并补全频率分布直方图;
(2)分别从两个小区随机选取1户家庭,求这两户家庭当日消费额在![]() 的户数为1时的概率(频率当作概率使用);
的户数为1时的概率(频率当作概率使用);
(3)运用所学统计知识分析比较两个小区的当日网购消费水平.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若点![]() 为点
为点![]() 在平面
在平面![]() 上的正投影,则记
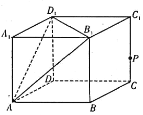
上的正投影,则记![]() .如图,在棱长为1的正方体
.如图,在棱长为1的正方体![]() 中,记平面
中,记平面![]() 为
为![]() ,平面
,平面![]() 为
为![]() ,点
,点![]() 是线段
是线段![]() 上一动点,
上一动点,![]() .给出下列四个结论:
.给出下列四个结论:
①![]() 为
为![]() 的重心;
的重心;
②![]() ;
;
③当![]() 时,
时,![]() 平面
平面![]() ;
;
④当三棱锥![]() 的体积最大时,三棱锥
的体积最大时,三棱锥![]() 外接球的表面积为
外接球的表面积为![]() .
.
其中,所有正确结论的序号是________________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为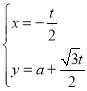 (
(![]() ,t为参数).以坐标原点为极点,
,t为参数).以坐标原点为极点,![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直角坐标系下直线![]() 与曲线
与曲线![]() 的普通方程;
的普通方程;
(2)设直线![]() 与曲线
与曲线![]() 交于点
交于点![]() 、
、![]() (二者可重合),交
(二者可重合),交![]() 轴于
轴于![]() ,若
,若![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出以下几个结论:
①命题![]() ,
,![]() ,则
,则![]() ,
,![]()
②命题“若![]() ,则
,则![]() ”的逆否命题为:“若
”的逆否命题为:“若![]() ,则
,则![]() ”
”
③“命题![]() 为真”是“命题
为真”是“命题![]() 为真”的充分不必要条件
为真”的充分不必要条件
④若![]() ,则
,则![]() 的最小值为4
的最小值为4
其中正确结论的个数是( )
A.1B.2C.3D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在![]() 中,
中,![]() ,
,![]() ,
,![]() 分别为内角
分别为内角![]() ,
,![]() ,
,![]() 的对边,且满
的对边,且满![]() .
.
(1)求![]() 的大小;
的大小;
(2)再在①![]() ,②
,②![]() ,③
,③![]() 这三个条件中,选出两个使
这三个条件中,选出两个使![]() 唯一确定的条件补充在下面的问题中,并解答问题.若________,________,求
唯一确定的条件补充在下面的问题中,并解答问题.若________,________,求![]() 的面积.
的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com