【题目】若点![]() 为点
为点![]() 在平面
在平面![]() 上的正投影,则记
上的正投影,则记![]() .如图,在棱长为1的正方体
.如图,在棱长为1的正方体![]() 中,记平面
中,记平面![]() 为
为![]() ,平面
,平面![]() 为
为![]() ,点
,点![]() 是线段
是线段![]() 上一动点,
上一动点,![]() .给出下列四个结论:
.给出下列四个结论:
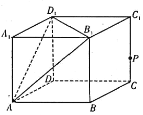
①![]() 为
为![]() 的重心;
的重心;
②![]() ;
;
③当![]() 时,
时,![]() 平面
平面![]() ;
;
④当三棱锥![]() 的体积最大时,三棱锥
的体积最大时,三棱锥![]() 外接球的表面积为
外接球的表面积为![]() .
.
其中,所有正确结论的序号是________________.
【答案】①②③
【解析】
①点![]() 在平面
在平面![]() 内的正投影为点
内的正投影为点![]() ,而正方体的体对角线与和它不相交的的面对角线垂直,所以直线
,而正方体的体对角线与和它不相交的的面对角线垂直,所以直线![]() 垂直于平面
垂直于平面![]() ,而
,而![]() 为正三角形,可得
为正三角形,可得![]() 为正三角形
为正三角形![]() 的重心,所以①是正确的;
的重心,所以①是正确的;
②取![]() 的中点
的中点![]() ,连接
,连接![]() ,则点
,则点![]() 在平面
在平面![]() 的正投影在
的正投影在![]() 上,记为
上,记为![]() ,而
,而![]() 平面
平面![]() 平面
平面![]() ,所以
,所以![]() ,所以②正确;
,所以②正确;
③若设![]() ,则由
,则由![]() 可得
可得![]() ,然后对应边成比例,可解
,然后对应边成比例,可解![]() ,所以③正确;
,所以③正确;
④由于![]() ,而
,而![]() 的面积是定值,所以当点
的面积是定值,所以当点![]() 到平面
到平面![]() 的距离最大时,三棱锥
的距离最大时,三棱锥![]() 的体积最大,而当点
的体积最大,而当点![]() 与点
与点![]() 重合时,点
重合时,点![]() 到平面
到平面![]() 的距离最大,此时
的距离最大,此时![]() 为棱长为
为棱长为![]() 的正四面体,其外接球半径
的正四面体,其外接球半径![]() ,则
,则![]() 球
球![]() ,所以④错误.
,所以④错误.
因为![]() ,连接
,连接![]() ,则有
,则有![]() 平面
平面![]() 平面
平面![]() 为正三角形,所以
为正三角形,所以![]() 为正三角形
为正三角形![]() 的中心,也是
的中心,也是![]() 的重心,所以①正确;
的重心,所以①正确;
由![]() 平面
平面![]() ,可知平面
,可知平面![]() 平面
平面![]() ,记
,记![]() ,
,
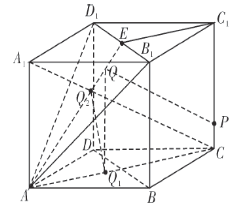
由![]() ,可得
,可得![]() 平面
平面![]() 平面
平面![]() ,则
,则![]() ,所以②正确;
,所以②正确;
若![]() 平面
平面![]() ,则
,则![]() ,设
,设![]() 由
由![]() 得
得![]() ,易得
,易得![]() ,由
,由![]() ,则
,则![]() ,由
,由![]() 得,
得,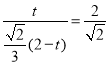 ,解得
,解得![]() ,所以③正确;
,所以③正确;
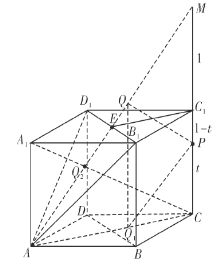
当![]() 与
与![]() 重合时,
重合时,![]() 最大,
最大,![]() 为棱长为
为棱长为![]() 的正四面体,其外接球半径
的正四面体,其外接球半径![]() ,则
,则![]() 球
球![]() ,所以④错误.
,所以④错误.
故答案为:①②③

