【题目】已知函数![]() ,给出下列结论:
,给出下列结论:
(1)若对任意![]() ,且
,且![]() ,都有
,都有![]() ,则
,则![]() 为R上的减函数;
为R上的减函数;
(2)若![]() 为R上的偶函数,且在
为R上的偶函数,且在![]() 内是减函数,
内是减函数, ![]() (-2)=0,则
(-2)=0,则![]() >0解集为(-2,2);
>0解集为(-2,2);
(3)若![]() 为R上的奇函数,则
为R上的奇函数,则![]() 也是R上的奇函数;
也是R上的奇函数;
(4)t为常数,若对任意的![]() ,都有
,都有![]() 则
则![]() 关于
关于![]() 对称。
对称。
其中所有正确的结论序号为_________
参考答案:
【答案】(1),(3)
【解析】对于(1),若对于对任意![]() ,且
,且![]() ,都有
,都有![]() ,即当
,即当![]() 时,
时, ![]() ,当
,当![]() 时,
时, ![]() ,则
,则![]() 为
为![]() 上的减函数,则(1)对;对于(2),若
上的减函数,则(1)对;对于(2),若![]() 为
为![]() 上的偶函数,且在
上的偶函数,且在![]() 内是减函数,则
内是减函数,则![]() 在
在![]() 上递增,
上递增, ![]() ,则
,则![]() 即为
即为![]() ,即有
,即有![]() ,解得
,解得![]() 或
或![]() ,则(2)错;对于(3),若
,则(2)错;对于(3),若![]() 为
为![]() 上的奇函数,则
上的奇函数,则![]() ,
, ![]() ,即有
,即有![]() 也是R上的奇函数,则(3)对;对于(4),若对任意的
也是R上的奇函数,则(3)对;对于(4),若对任意的![]() 都有
都有![]() ,即有
,即有![]() ,即
,即![]() 为周期函数,并非对称函数,若
为周期函数,并非对称函数,若![]() 满足
满足![]() ,则
,则![]() 关于直线
关于直线![]() 对称,则(4)错,故答案为(1)(3).
对称,则(4)错,故答案为(1)(3).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
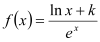 (
(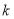 为常数,
为常数,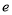 =2.71828……是自然对数的底数),曲线
=2.71828……是自然对数的底数),曲线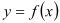 在点
在点 处的切线与
处的切线与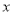 轴平行.
轴平行.(1)求
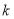 的值;
的值;(2)求
 的单调区间;
的单调区间;(3)设
 ,其中
,其中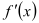 是
是 的导函数.证明:对任意
的导函数.证明:对任意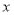 >0,
>0,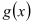 <
<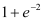 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】在棱长均相等的正三棱柱ABCA1B1C1中,D为BB1的中点,F在AC1上,且DF⊥AC1,则下述结论:
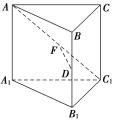
①AC1⊥BC;
②AF=FC1;
③平面DAC1⊥平面ACC1A1,其中正确的个数为( )
A.0 B.1
C.2 D.3
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数
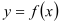 的图像经过坐标原点,其到函数为
的图像经过坐标原点,其到函数为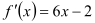 ,数列的前
,数列的前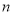 项和为
项和为 ,点
,点
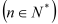 均在函数
均在函数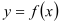 的图像上.
的图像上. (I)求数列
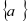 的通项公式;
的通项公式;(Ⅱ)设
 ,
, 是数列
是数列 的前
的前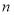 n项和,求使得
n项和,求使得 <
<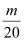 对所有都成立的最小正整数m.
对所有都成立的最小正整数m. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥PABCD中,侧面PAB⊥底面ABCD,底面ABCD为矩形,PA=PB,O为AB的中点,OD⊥PC.
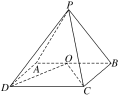
(1)求证:OC⊥PD;
(2)若PD与平面PAB所成的角为30°,求二面角DPCB的余弦值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】5名男生4名女生站成一排,求满足下列条件的排法:
(1)女生都不相邻有多少种排法?
(2)男生甲、乙、丙排序一定(只考虑位置的前后顺序),有多少种排法?
(3)男甲不在首位,男乙不在末位,有多少种排法?
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于函数f(x),若存在x0∈R,使得f(x0)=x0成立,则称x0为f(x)的天宫一号点.已知函数f(x)=ax2+(b-7)x+18的两个天宫一号点分别是-3和2.
(1)求a,b的值及f(x)的表达式;
(2)当函数f(x)的定义域是[t,t+1]时,求函数f(x)的最大值g(t).
相关试题

