【题目】设函数 ![]() (x∈R),其中t∈R,将f(x)的最小值记为g(t).
(x∈R),其中t∈R,将f(x)的最小值记为g(t).
(1)求g(t)的表达式;
(2)当﹣1≤t≤1时,要使关于t的方程g(t)=kt有且仅有一个实根,求实数k的取值范围
参考答案:
【答案】
(1)解:由已知有: ![]() =sin2x﹣2tsinx+2t2﹣6t+1=(sinx﹣t)2+t2﹣6t+1,
=sin2x﹣2tsinx+2t2﹣6t+1=(sinx﹣t)2+t2﹣6t+1,
由于x∈R,∴﹣1≤sinx≤1,
∴当t<﹣1时,则当sinx=﹣1时,f(x)min=2t2﹣4t+2;
当﹣1≤t≤1时,则当sinx=t时,f(x)min=t2﹣6t+1;
当t>1时,则当sinx=1时,f(x)min=2t2﹣8t+2;
综上, 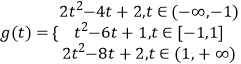
(2)解:当﹣1≤t≤1时,g(t)=t2﹣6t+1,方程g(t)=kt即t2﹣6t+1=kt,
即方程t2﹣(k+6)t+1=0在区间[﹣1,1]有且仅有一个实根,
令q(t)=t2﹣(k+6)t+1,则有:
①若△=(k+6)2﹣4=0,即k=﹣4或k=﹣8.
当k=﹣4时,方程有重根t=1;当k=﹣8时,c方程有重根t=﹣1,∴k=﹣4或k=﹣8.
② 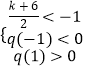
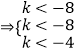 k<﹣8或
k<﹣8或 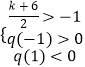
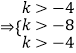 k>﹣4,
k>﹣4,
综上,当k∈(﹣∞,﹣8]∪[﹣4,+∞)时,关于t的方程g(t)=kt在区间[﹣1,1]有且仅有一个实根
【解析】(1)首先对函数f(x)进行化简整理,进而看当t<﹣1,﹣1≤t≤1和t>1时时函数f(x)的最小值,进而确定g(t)的解析式.(2)根据(1)可知当﹣1≤t≤1时函数g(t)的解析式,整理g(t)=kt得t2﹣(k+6)t+1=0问题转化为在区间[﹣1,1]有且仅有一个实根,先根据判别式等于0求得k的值,令q(t)=t2﹣(k+6)t+1,进而确定函数与x轴的轴有一个交点落在区间[﹣1,1]分别求得k的范围,最后综合可得答案.
【考点精析】根据题目的已知条件,利用函数的最值及其几何意义的相关知识可以得到问题的答案,需要掌握利用二次函数的性质(配方法)求函数的最大(小)值;利用图象求函数的最大(小)值;利用函数单调性的判断函数的最大(小)值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】直线x+y-1=0被圆(x+1)2+y2=3截得的弦长等于( )
A.
 B. 2
B. 2C. 2
 D. 4
D. 4 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=sin(ωx+)(ω>0,0≤≤π)为偶函数,其图象上相邻的两个最高点之间的距离为2π. (Ⅰ)求f(x)的解析式;
(Ⅱ)若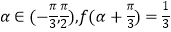 ,求
,求 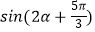 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】设椭圆C:
 的左焦点为F,过点F的直线与椭圆C相交于A,B两点,直线l的倾斜角为60°,
的左焦点为F,过点F的直线与椭圆C相交于A,B两点,直线l的倾斜角为60°,  .
. 
(1)求椭圆C的离心率;
(2)如果|AB|= ,求椭圆C的方程.
,求椭圆C的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知棱长都相等的正三棱锥内接于一个球,某学生画出四个过球心的平面截球与正三棱锥所得的图形,如图所示,则( )
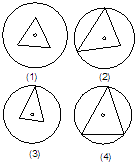
A.以上四个图形都是正确的
B.只有(2)(4)是正确的
C.只有(4)是错误的
D.只有(1)(2)是正确的 -
科目: 来源: 题型:
查看答案和解析>>【题目】若两条异面直线所成的角为90°,则称这对异面直线为“理想异面直线对”,在连接正方体各顶点的所有直线中,“理想异面直线对”的对数为( )
A.24
B.48
C.72
D.78 -
科目: 来源: 题型:
查看答案和解析>>【题目】直线过点P
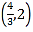 且与x轴、y轴的正半轴分别交于A,B两点,O为坐标原点,是否存在这样的直线满足下列条件:①△AOB的周长为12;②△AOB的面积为6.若存在,求出方程;若不存在,请说明理由.
且与x轴、y轴的正半轴分别交于A,B两点,O为坐标原点,是否存在这样的直线满足下列条件:①△AOB的周长为12;②△AOB的面积为6.若存在,求出方程;若不存在,请说明理由.
相关试题

