【题目】已知函数![]() .
.
(1)求曲线![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(2)求函数![]() 的单调区间及极值;
的单调区间及极值;
(3)对![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() 单调递减区间为
单调递减区间为![]() ,单调递增区间为
,单调递增区间为![]() ,极小值为
,极小值为![]() ,无极大值;(3)
,无极大值;(3)![]() .
.
【解析】
试题分析:(1)由题意切点为![]() ,求导可得斜率,即可写出切线方程;(2)对函数
,求导可得斜率,即可写出切线方程;(2)对函数![]() 求导,判断导函数的正负情况,写出单调区间及极值;(3)对
求导,判断导函数的正负情况,写出单调区间及极值;(3)对![]() 成立,即
成立,即![]() ,构造函数
,构造函数
![]() ,求导分别对
,求导分别对![]() 和
和![]() 分类讨论,
分类讨论,![]() 单调递增舍去,
单调递增舍去,![]() 时再按
时再按![]() 和
和![]() 分两种情况分别研究单调性和最值,比较最值和
分两种情况分别研究单调性和最值,比较最值和![]() 的大小关系,求出
的大小关系,求出![]() 的范围.
的范围.
试题解析:解:(1)由题意知![]() 的定义域为
的定义域为![]() 且
且![]() ,
,
又∵![]() ,
,
故切线方程为![]() .
.
(2)![]() ,
,
![]() ,
,
当![]() 时,则
时,则![]() ,
,
此时![]() 在
在![]() 上单调递减.
上单调递减.
当![]() 时,则
时,则![]() ,此时
,此时![]() ,
,
![]() 在
在![]() 上单调递增.
上单调递增.
故![]() 在单调递减区间为
在单调递减区间为![]() ,单调递增区间为
,单调递增区间为![]() .
.
当![]() 时,
时,![]() 取极小值,且
取极小值,且![]() 极小值为-2,
极小值为-2,![]() 无极大值
无极大值
(3)对![]() 成立,即
成立,即![]() ,
,
令![]() ,
,
则当![]() 时,
时,![]() 恒成立.
恒成立.
因为![]() .
.
①当![]() 时,
时,![]() ,
,![]() 在
在![]() 上单调递增,故
上单调递增,故![]() ,
,
这与![]() 恒成立矛盾
恒成立矛盾
②当![]() 时,二次方程
时,二次方程![]() 的判别式
的判别式![]() ,令
,令![]() ,解得
,解得![]() ,此时
,此时![]() 在
在![]() 上单调递减.
上单调递减.
故![]() ,满足
,满足![]() 恒成立.
恒成立.
由![]() 得
得![]() ,方程
,方程![]() 的两根分别是
的两根分别是
![]() ,其中
,其中![]() ,
,
当![]() 时,
时,![]() 在
在![]() 上单调递增,
上单调递增,![]() ,
,
这与![]() 恒成立矛盾.
恒成立矛盾.
综上可知:![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】某城市100户居民的月平均用电量(单位:度),以
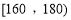 ,
, ,
,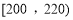 ,
,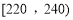 ,
, ,
,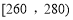 ,
,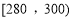 分组的频率分布直方图如图:
分组的频率分布直方图如图: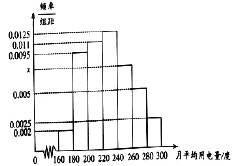
(Ⅰ)求直方图中
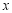 的值;
的值;(Ⅱ)求月平均用电量的众数和中位数;
(Ⅲ)在月平均用电量为
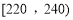 ,
, ,
,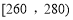 ,
,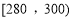 的四组用户中,用分层抽样的方法抽取11户居民,则月平均用电量在
的四组用户中,用分层抽样的方法抽取11户居民,则月平均用电量在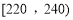 的用户中应抽取多少户?
的用户中应抽取多少户? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数
 为常数,
为常数, 的一个零点是
的一个零点是 ,函数
,函数 是自然对数的底数, 设函数
是自然对数的底数, 设函数 .
.(1)过点坐标原点
 作曲线
作曲线 的切线, 证明切点的横坐标为
的切线, 证明切点的横坐标为 ;
;(2)令
 ,若函数
,若函数 在区间
在区间 上是单调函数, 求
上是单调函数, 求 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知过点
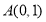 且斜率为
且斜率为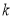 的直线
的直线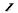 与圆
与圆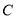 :
: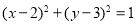 交于点
交于点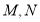 两点.
两点.(1)求
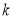 的取值范围;
的取值范围;(2)请问是否存在实数k使得
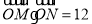 (其中
(其中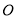 为坐标原点),如果存在请求出k的值,并求
为坐标原点),如果存在请求出k的值,并求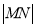 ;如果不存在,请说明理由。
;如果不存在,请说明理由。 -
科目: 来源: 题型:
查看答案和解析>>【题目】某公司生产一批
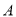 产品需要原材料500吨,每吨原材料可创造利润12万元,该公司通过设备升级,生产这批
产品需要原材料500吨,每吨原材料可创造利润12万元,该公司通过设备升级,生产这批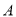 产品所需原材料减少了
产品所需原材料减少了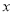 吨,且每吨原材料创造的利润提高
吨,且每吨原材料创造的利润提高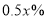 ;若将少用的
;若将少用的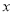 吨原材料全部用于生产公司新开发的
吨原材料全部用于生产公司新开发的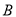 产品,每吨原材料创造的利润为
产品,每吨原材料创造的利润为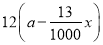 万元
万元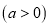 .
.(1)若设备升级后生产这批
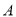 产品的利润不低于原来生产该批
产品的利润不低于原来生产该批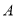 产品的利润,求
产品的利润,求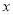 的取值范围;
的取值范围;(2)若生产这批
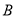 产品的利润始终不高于设备升级后生产这批
产品的利润始终不高于设备升级后生产这批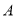 产品的利润,求
产品的利润,求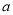 的最大值.
的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某校从高二年级学生中随机抽取50名学生,将他们的期中考试数学成绩(满分100分,成绩均为不低于40分的整数)分成六段:[40,50),[50,60),…,[90,100],得到如图所示的频率分布直方图.
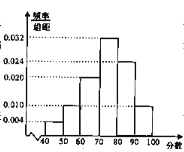
(1)若该校高二年级共有学生1000人,试估计成绩不低于60分的人数;
(2)求该校高二年级全体学生期中考试成绩的众数、中位数和平均数的估计值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】正方体
 的棱长为1,
的棱长为1, 分别是棱
分别是棱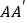 ,
, 的中点,过直线
的中点,过直线 的平面分别与棱
的平面分别与棱 、
、 交于
交于 ,设
,设 ,
, ,给出以下四个命题:
,给出以下四个命题:①四边形
 为平行四边形;
为平行四边形;②若四边形
 面积
面积 ,
, ,则
,则 有最小值;
有最小值;③若四棱锥
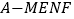 的体积
的体积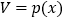
 ,
, ,则
,则 为常函数;
为常函数;④若多面体
 的体积
的体积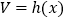 ,
, ,则
,则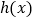 为单调函数.
为单调函数.其中假命题为( )
A. ① ③ B. ② C. ③④ D. ④
相关试题

