【题目】函数![]() 的图象为C,如下结论中正确的是( )
的图象为C,如下结论中正确的是( )
①图象C关于直线![]() 对称;②函数
对称;②函数![]() 在区间
在区间![]() 内是增函数;
内是增函数;
③图象C关于点![]() 对称;④由
对称;④由![]() 的图象向右平移
的图象向右平移![]() 个单位长度可以得到图象C
个单位长度可以得到图象C
A.①③B.②③C.①②③D.①②
参考答案:
【答案】C
【解析】
先通过三角公式将函数变形为![]() 的形式,
的形式,
①直接利用整体思想求出函数的对称轴方程,根据![]() 的取值求得结果.
的取值求得结果.
②直接利用整体思想求出函数的单调区间,根据![]() 的取值求得结果.
的取值求得结果.
③直接利用整体思想求出函数的对称中心,根据![]() 的取值求得结果.
的取值求得结果.
④直接利用函数的平移变换求得结果.
解:![]()
①令:![]() ,解得:
,解得:![]() ,
,
当![]() 时,图象
时,图象![]() 关于直线
关于直线![]() 对称,所以①正确.
对称,所以①正确.
②令:![]() ,
,
解得:![]() ,
,
当![]() 时,函数
时,函数![]() 在区间
在区间![]() 内是增函数;所以②正确.
内是增函数;所以②正确.
③令:![]() ,解得:
,解得:![]() ,
,
当![]() 时,图象
时,图象![]() 关于点
关于点![]() 对称.所以③正确.
对称.所以③正确.
④将![]() 的图象向右平移
的图象向右平移![]() 个单位,得到的函数解析式为
个单位,得到的函数解析式为![]() ,所以④错误.
,所以④错误.
故选:C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】港珠澳大桥于2018年10月24日正式通车,它是中国境内一座连接香港、珠海和澳门的桥隧工程,桥隧全长55千米,桥面为双向六车道高速公路,大桥通行限速100 km/h. 现对大桥某路段上汽车行驶速度进行抽样调查,画出频率分布直方图(如图).根据直方图估计在此路段上汽车行驶速度的众数和行驶速度超过90 km/h的概率分别为

A.
 ,
, B.
B.  ,
,
C.
 ,
, D.
D.  ,
,
-
科目: 来源: 题型:
查看答案和解析>>【题目】某电视台为宣传本市,随机对本市内
 岁的人群抽取了
岁的人群抽取了 人,回答问题“本市内著名旅游景点有哪些” ,统计结果如图表所示.
人,回答问题“本市内著名旅游景点有哪些” ,统计结果如图表所示.组号
分组
回答正确的人数
回答正确的人数占本组的频率
第1组
[15,25)
a
0.5
第2组
[25,35)
18
x
第3组
[35,45)
b
0.9
第4组
[45,55)
9
0.36
第5组
[55,65]
3
y

(1)分别求出
 的值;
的值;(2)根据频率分布直方图估计这组数据的中位数(保留小数点后两位)和平均数;
(3)若第1组回答正确的人员中,有2名女性,其余为男性,现从中随机抽取2人,求至少抽中1名女性的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是某公司2001年至2017年新产品研发费用
 (单位:万元)的折线图.为了预测该公司2019年的新产品研发费用,建立了
(单位:万元)的折线图.为了预测该公司2019年的新产品研发费用,建立了 与时间变量
与时间变量 的两个线性回归模型.根据2001年至2017年的数据(时间变量
的两个线性回归模型.根据2001年至2017年的数据(时间变量 的值依次为1,2,…,17)建立模型①:
的值依次为1,2,…,17)建立模型①: ;根据2011年至2017年的数据(时间变量
;根据2011年至2017年的数据(时间变量 的值依次为1,2,…,7)建立模型②:
的值依次为1,2,…,7)建立模型②: .
.
(1)分别利用这两个模型,求该公司2019年的新产品研发费用的预测值;
(2)你认为用哪个模型得到的预测值更可靠?并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆

 的离心率为
的离心率为 ,且过点
,且过点 .直线
.直线 与
与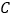 交于
交于 ,
, 两点,点
两点,点 是
是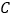 的左焦点.
的左焦点.(1)求椭圆
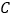 的方程;
的方程;(2)若
 过点
过点 且不与
且不与 轴重合,求
轴重合,求 面积
面积 的最大值.
的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某同学用“五点法”画函数
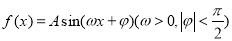 在某一个周期内的图象时,列表并填入了部分数据,如下表:
在某一个周期内的图象时,列表并填入了部分数据,如下表:
0
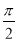







0
5

0
(1)请将上表数据补充完整,填写在答题卡上相应位置,并直接写出函数
 的解析式;
的解析式;(2)将
 图象上所有点向左平行移动
图象上所有点向左平行移动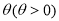 个单位长度,并把图象上所有点的横坐标缩短为原来的
个单位长度,并把图象上所有点的横坐标缩短为原来的 (纵坐标不变),得到
(纵坐标不变),得到 的图象.若
的图象.若 图象的一个对称中心为
图象的一个对称中心为 ,求
,求 的最小值;
的最小值;(3)在(2)条件下,求
 在
在 上的增区间.
上的增区间. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知向量
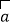 = (1,2sinθ),
= (1,2sinθ), = (sin(θ+
= (sin(θ+ ),1),θ
),1),θ R。
R。(1) 若
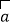 ⊥
⊥ ,求 tanθ的值;
,求 tanθ的值;(2) 若
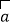 ∥
∥ ,且 θ
,且 θ (0,
(0, ),求 θ的值
),求 θ的值
相关试题

