【题目】一个化肥厂生产甲、乙两种混合肥料,生产1车皮甲种肥料的主要原料是磷酸盐4t,硝酸盐18t;生产1车乙种肥料的主要原料是磷酸盐1t、硝酸盐15t.现库存磷酸盐10t、硝酸盐66t.已知生产1车皮甲种肥料,产生的利润为10000元;生产1车皮乙种肥料,产生的利润为5000元.那么分别生产甲、乙两种肥料各多少车皮,能够产生最大利润?最大利润是多少?
参考答案:
【答案】解:设x、y分别为计划生产甲、乙两种混合肥料的车皮数,于是满足以下条件:  ;
;
再设分别生产甲、乙两种肥料各x、y车皮产生
的利润为z=10000x+5000y=5000(2x+y),
由 ![]() 得两直线的交点M(2,2).
得两直线的交点M(2,2).
令t=2x+y,当直线L:y=﹣2x+t经过点M(2,2)时,它在y轴上的截距有最大值为6,此时z=30000.
∴分别生产甲、乙两种肥料各为2,2车皮,能够产生最大利润,最大利润是30000t.
【解析】先设x、y分别为计划生产甲、乙两种混合肥料的车皮数,根据题意列出约束条件,再利用线性规划的方法求解最优解即可.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设{an}为等差数列,Sn是其前n项和,已知S7=7,S15=75,Tn为数列{
 }的前n项和,
}的前n项和,
(1)求a1和d;
(2)求Tn . -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=
 x2+ax+1(a∈R). (Ⅰ)当a=
x2+ax+1(a∈R). (Ⅰ)当a=  时,求不等式f(x)<3的解集;
时,求不等式f(x)<3的解集;
(Ⅱ)当0<x<2时,不等式f(x)>0恒成立,求实数a的取值范围;
(Ⅲ)求关于x的不等式f(x)﹣ a2﹣1>0的解集.
a2﹣1>0的解集. -
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:极坐标与参数方程
在平面直角坐标系xoy中,曲线
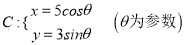 ,直线
,直线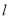 过点
过点 与曲线
与曲线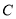 交于
交于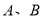 二点,
二点, 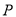 为
为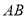 中点.以坐标原点O为极点,x轴正半轴为极轴,以平面直角坐标系xoy的单位1为基本单位建立极坐标系.
中点.以坐标原点O为极点,x轴正半轴为极轴,以平面直角坐标系xoy的单位1为基本单位建立极坐标系.(1)求直线
 的极坐标方程;
的极坐标方程;(2)
 为曲线
为曲线 上的动点,求
上的动点,求 的范围.
的范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知正四面体ABCD中,E是AB的中点,则异面直线CE与BD所成角的余弦值为( )
A.
B.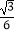
C.
D.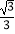
-
科目: 来源: 题型:
查看答案和解析>>【题目】综合题。
(1)已知点A(﹣1,﹣2)和B(﹣3,6),直线l经过点P(1,﹣5).且与直线AB平行,求直线l的方程
(2)求垂直于直线x+3y﹣5=0,且与点P(﹣1,0)的距离是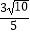 的直线m的方程.
的直线m的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,梯形ABEF中,AF∥BE,AB⊥AF,且AB=BC=AD=DF=2CE=2,沿DC将梯形DCFE折起,使得平面DCFE⊥平面ABCD.
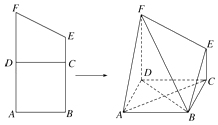
(1)证明:AC∥平面BEF;
(2)求三棱锥D﹣BEF的体积;
(3)求直线AF与平面BDF所求的角.
相关试题

