【题目】已知函数![]() ,
,![]() .
.
(1)若曲线![]() 在
在![]() 处的切线方程为
处的切线方程为![]() ,求实数
,求实数![]() 的值;
的值;
(2)设![]() ,若对任意两个不等的正数
,若对任意两个不等的正数![]() ,
,![]() ,都有
,都有![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(3)若在![]() 上存在一点
上存在一点![]() ,使得
,使得![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】
试题分析:(1)借助题设条件运用导数的几何意义建立方程求解;(2)借助题设运用转化化归的思想进行转化再运用导数知识求解;(3)依据题设先将问题进行转化,再借助导数知识分类整合思想分类探求求解.
试题解析:
(1)由![]()
![]() ,得
,得![]() ,
,
由题意![]() ,所以
,所以![]() .
.
(2)![]() ,
,
因为对任意两个不等的正数![]() ,
,![]() ,都有
,都有![]() ,
,
设![]() ,则
,则![]() ,即
,即![]() 恒成立,
恒成立,
问题等价于函数![]() ,即
,即![]() 在
在![]() 为增函数,
为增函数,
所以![]() 在
在![]() 上恒成立,即
上恒成立,即![]() 在
在![]() 上恒成立,
上恒成立,
所以![]() ,即实数
,即实数![]() 的取值范围是
的取值范围是![]() .
.
(3)不等式![]() 等价于
等价于![]() ,
,
整理得![]() ,
,
设![]() ,由题意知,在
,由题意知,在![]() 上存在一点
上存在一点![]() ,使得
,使得![]() ,
,
由![]() ,
,
因为![]() ,所以
,所以![]() ,令
,令![]() ,得
,得![]() .
.
①当![]() ,即
,即![]() 时,
时,![]() 在
在![]() 上单调递增,
上单调递增,
只需![]() ,解得
,解得![]() .
.
②当![]() ,即
,即![]() 时,
时,![]() 在
在![]() 处取最小值,
处取最小值,
令![]() ,即
,即![]() ,可得
,可得![]() ,
,
考查式子![]() ,因为
,因为![]() ,可得左端大于1,而右端小于1,所以不等式不可能成立.
,可得左端大于1,而右端小于1,所以不等式不可能成立.
③当![]() ,即
,即![]() 时,
时,![]() 在
在![]() 上单调递减,
上单调递减,
只需![]() ,解得
,解得![]() .
.
综上所述,实数![]() 的取值范围是
的取值范围是![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥
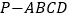 中,底面
中,底面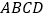 为平行四边形,
为平行四边形, 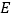 为侧棱
为侧棱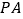 的中点.
的中点.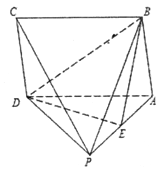
(Ⅰ)求证:
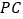 ∥平面
∥平面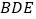
(Ⅱ)若
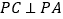 ,
,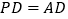 ,
,求证:平面
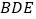
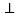 平面
平面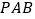
-
科目: 来源: 题型:
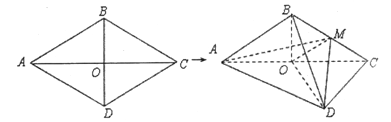
查看答案和解析>>【题目】如图,棱形
 的边长为6,
的边长为6, 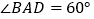 ,
,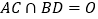 .将棱形
.将棱形 沿对角线
沿对角线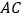 折起,得到三棱锥
折起,得到三棱锥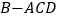 ,点
,点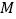 是棱
是棱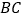 的中点,
的中点, 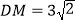 .
.
(Ⅰ)求证:
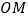 ∥平面
∥平面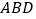 ;
;(Ⅱ)求三棱锥
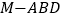 的体积.
的体积. -
科目: 来源: 题型:
查看答案和解析>>【题目】“奶茶妹妹”对某时间段的奶茶销售量及其价格进行调查,统计出售价
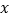 元和销售量
元和销售量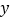 杯之间的一组数据如下表所示:
杯之间的一组数据如下表所示:价格
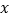
5
5.5
6.5
7
销售量
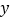
12
10
6
4
通过分析,发现销售量
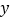 对奶茶的价格
对奶茶的价格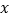 具有线性相关关系.
具有线性相关关系.(Ⅰ)求销售量
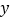 对奶茶的价格
对奶茶的价格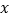 的回归直线方程;
的回归直线方程;(Ⅱ)欲使销售量为
 杯,则价格应定为多少?
杯,则价格应定为多少?附:线性回归方程为
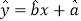 ,其中
,其中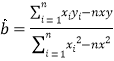 ,
,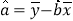
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
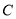 :
: 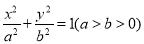 的左、右焦点分别为
的左、右焦点分别为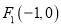 ,
, 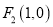 ,点
,点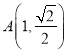 在椭圆
在椭圆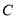 上.
上.(Ⅰ)求椭圆
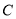 的标准方程;
的标准方程;(Ⅱ)是否存在斜率为2的直线
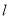 ,使得当直线
,使得当直线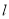 与椭圆
与椭圆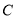 有两个不同交点
有两个不同交点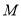 、
、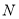 时,能在直线
时,能在直线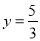 上找到一点
上找到一点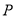 ,在椭圆
,在椭圆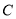 上找到一点
上找到一点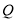 ,满足
,满足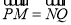 ?若存在,求出直线
?若存在,求出直线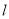 的方程;若不存在,说明理由.
的方程;若不存在,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆
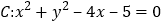 .
.(1)判断圆
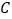 与圆
与圆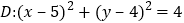 的位置关系,并说明理由;
的位置关系,并说明理由;(2)若过点
 的直线 与圆
的直线 与圆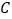 相切,求直线的方程.
相切,求直线的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】海关对同时从
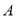 ,
,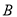 ,
,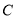 三个不同地区进口的某种商品进行抽样检测,从各地区进口此种商品的数量(单位:件)如下表所示.工作人员用分层抽样的方法从这些商品中共抽取6件样品进行检测.
三个不同地区进口的某种商品进行抽样检测,从各地区进口此种商品的数量(单位:件)如下表所示.工作人员用分层抽样的方法从这些商品中共抽取6件样品进行检测.地区
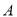
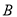
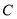
数量
50
150
100
(1)求这6件样品中来自
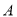 ,
, ,
,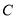 各地区商品的数量;
各地区商品的数量;(2)若在这6件样品中随机抽取2件送往甲机构进行进一步检测,求这2件商品来自相同地区的概率.
相关试题

