【题目】如图茎叶图记录了甲、乙两组各四名同学的植树棵树.乙组记录中有一个数据模糊,无法确认,在图中以X表示.
(注:方差 ![]() ,其中
,其中 ![]() 为x1 , x2 , …xn的平均数)
为x1 , x2 , …xn的平均数)
(1)如果X=8,求乙组同学植树棵树的平均数和方差;
(2)如果X=9,分别从甲、乙两组中随机选取一名同学,求这两名同学的植树总棵数为19的概率.
参考答案:
【答案】
(1)解:当X=8时,由茎叶图可知,乙组同学的植树棵数是:8,8,9,10,所以平均数为 ![]() =
= ![]()
方差为s2= ![]() [
[ ![]() +
+ ![]() +
+ ![]() +
+ ![]() ]=
]= ![]()
(2)解:记甲组四名同学为A1,A2,A3,A4,他们植树的棵数依次为9,9,11,11;乙组四名同学为B1,B2,B3,B4,他们植树的棵数依次为9,8,9,10,分别从甲、乙两组中随机选取一名同学,所有可能的结果有16个,它们是:
(A1,B1),(A1,B2),(A1,B3),(A1,B4),
(A2,B1),(A2,B2),(A2,B3),(A2,B4),
(A3,B1),(A2,B2),(A3,B3),(A1,B4),
(A4,B1),(A4,B2),(A4,B3),(A4,B4),
用C表示:“选出的两名同学的植树总棵数为19”这一事件,则C中的结果有4个,它们是:(A1,B4),(A2,B4),(A3,B2),(A4,B2),故所求概率为P(C)= ![]() =
= ![]()
【解析】(1)当X=8时,由茎叶图可知,乙组同学的植树棵数是:8,8,9,10,由此能求出乙组同学植树棵树的平均数和方差;(2)先求出从甲、乙两组中随机选取一名同学,所有可能的结果,再求出选出的两名同学的植树总棵数为19的结果数,由此可得概率.
【考点精析】关于本题考查的茎叶图,需要了解茎叶图又称“枝叶图”,它的思路是将数组中的数按位数进行比较,将数的大小基本不变或变化不大的位作为一个主干(茎),将变化大的位的数作为分枝(叶),列在主干的后面,这样就可以清楚地看到每个主干后面的几个数,每个数具体是多少才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两袋中各装有大小相同的小球9个,其中甲袋中红色、黑色、白色小球的个数分别为2、3、4,乙袋中红色、黑色、白色小球的个数均为3,某人用左右手分别从甲、乙两袋中取球.
(1)若左右手各取一球,求两只手中所取的球颜色不同的概率;
(2)若左右手依次各取两球,称同一手中两球颜色相同的取法为成功取法,记两次取球的成功取法次数为随机变量
 ,求
,求 的分布列和数学期望.
的分布列和数学期望. -
科目: 来源: 题型:
查看答案和解析>>【题目】某研究机构对高三学生的记忆力x和判断力y进行统计分析,所得数据如表所示:
x
6
8
10
12
y
2
3
5
6
画出上表数据的散点图如图所示
(其中 ,
,  =
= 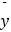 ﹣
﹣ 
 )
)
(1)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程 =
=  x+
x+  .
.
(2)试根据(1)求出的线性回归方程,预测记忆力为9的学生的判断力 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知a>0,集合A={x|ax2﹣2x+2a﹣1=0},B={y|y=log2(x+
 ﹣4)},p:A=,q:B=R.
﹣4)},p:A=,q:B=R.
(1)若p∧q为真,求a的最大值;
(2)若p∧q为为假,p∨q为真,求a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】在四棱锥P﹣ABCD中,PA⊥面ABCD,∠DAB=90°,AB平行于CD,AD=CD=2AB=2,E,F分别为PC,CD的中点
(1)求证:AB⊥面BEF;
(2)设PA=h,若二面角E﹣BD﹣C大于45°,求h的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形
 与梯形
与梯形 所在的平面互相垂直,
所在的平面互相垂直, 
 为
为 的中点.
的中点.(1)求证:
 平面
平面 ;
;(2)求证:
 平面
平面 ;
;(3)求平面
 与平面
与平面 所成锐二面角的余弦值.
所成锐二面角的余弦值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】《莱因德纸草书》(Rhind Papyrus)是世界上最古老的数学著作之一,书中有这样一道题:把120个面包分成5份,使每份的面包数成等差数列,且较多的三份之和恰好是较少的两份之和的7倍,则最少的那份有( )个面包.
A.4
B.3
C.2
D.1
相关试题

