【题目】已知函数f(x)=loga(1+x),g(x)=loga(1﹣x)其中(a>0且a≠1),设h(x)=f(x)﹣g(x).
(1)求函数h(x)的定义域,判断h(x)的奇偶性,并说明理由;
(2)若f(3)=2,求使h(x)<0成立的x的集合.
参考答案:
【答案】
(1)解:由题意,得 ![]()
解得﹣1<x<1
故h(x)的定义域为(﹣1,1).
h(x)的定义域为(﹣1,1),关于数0对称,
且h(﹣x)=f(﹣x)﹣g(﹣x)=loga(1﹣x)﹣loga(1+x)=﹣h(x)
故h(x)为奇函数
(2)解:由f(3)=2得a=2
![]()
即 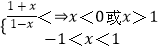 ,
,
解得﹣1<x<0
∴所求的x的集合{x|﹣1<x<0}
【解析】(1)求函数h(x)的定义域,即是使得函数f(x),g(x)都有意义的条件,从而可得,利用函数奇偶函数的定义检验h(﹣x)与h(x)的关系可判断函数的奇偶性(2)由f(3)=2得a=2,根据对数的运算性质可得h(x),代入解不等式即可
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知{an}为等差数列,前n项和为Sn(n∈N*),{bn}是首项为2的等比数列,且公比大于0,b2+b3=12,b3=a4-2a1,S11=11b4.
(Ⅰ)求{an}和{bn}的通项公式;
(Ⅱ)求数列{a2nbn}的前n项和(n∈N*).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=(
 )x的图象与函数g(x)的图象关于直线y=x对称,令h(x)=g(1﹣|x|),则关于h(x)有下列命题:
)x的图象与函数g(x)的图象关于直线y=x对称,令h(x)=g(1﹣|x|),则关于h(x)有下列命题:
①h(x)的图象关于原点对称;
②h(x)为偶函数;
③h(x)的最小值为0;
④h(x)在(0,1)上为减函数.
其中正确命题的序号为: . -
科目: 来源: 题型:
查看答案和解析>>【题目】已知集合A={x|x2﹣2x﹣8≤0},B={x|
 <0},U=R.
<0},U=R.
(1)求A∪B;
(2)求(UA)∩B;
(3)如果C={x|x﹣a>0},且A∩C≠,求a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=
 .
.
(1)用定义证明函数f(x)在(﹣∞,+∞)上为减函数;
(2)若x∈[1,2],求函数f(x)的值域;
(3)若g(x)= ,且当x∈[1,2]时g(x)≥0恒成立,求实数a的取值范围.
,且当x∈[1,2]时g(x)≥0恒成立,求实数a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知焦距为2的椭圆W:
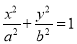 (a>b>0)的左、右焦点分别为A1,A2,上、下顶点分别为B1,B2,点M(x0,y0)为椭圆W上不在坐标轴上的任意一点,且四条直线MA1,MA2,MB1,MB2的斜率之积为
(a>b>0)的左、右焦点分别为A1,A2,上、下顶点分别为B1,B2,点M(x0,y0)为椭圆W上不在坐标轴上的任意一点,且四条直线MA1,MA2,MB1,MB2的斜率之积为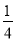 .
. 
(1)求椭圆W的标准方程;
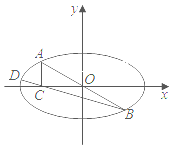
(2)如图所示,点A,D是椭圆W上两点,点A与点B关于原点对称,AD⊥AB,点C在x轴上,且AC与x轴垂直,求证:B,C,D三点共线.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某品牌茶壶的原售价为80元/个,今有甲、乙两家茶具店销售这种茶壶,甲店用如下方法促销:如果只购买一个茶壶,其价格为78元/个;如果一次购买两个茶壶,其价格为76元/个;…,一次购买的茶壶数每增加一个,那么茶壶的价格减少2元/个,但茶壶的售价不得低于44元/个;乙店一律按原价的75%销售.现某茶社要购买这种茶壶x个,如果全部在甲店购买,则所需金额为y1元;如果全部在乙店购买,则所需金额为y2元.
(1)分别求出y1、y2与x之间的函数关系式;
(2)该茶社去哪家茶具店购买茶壶花费较少?
相关试题

