【题目】“![]() ”是“对任意的正数
”是“对任意的正数![]() ,
, ![]() ”的( )
”的( )
A. 充分不必要条件 B. 必要不充分条件 C. 充要条件 D. 既不充分也不必要条件
【答案】A
【解析】分析:根据基本不等式,我们可以判断出“![]() ”?“对任意的正数x,2x+
”?“对任意的正数x,2x+![]() ≥1”与“对任意的正数x,2x+
≥1”与“对任意的正数x,2x+![]() ≥1”?“a=
≥1”?“a=
”真假,进而根据充要条件的定义,即可得到结论.
解答:解:当“a=![]() ”时,由基本不等式可得:
”时,由基本不等式可得:
“对任意的正数x,2x+![]() ≥1”一定成立,
≥1”一定成立,
即“a=![]() ”?“对任意的正数x,2x+
”?“对任意的正数x,2x+![]() ≥1”为真命题;
≥1”为真命题;
而“对任意的正数x,2x+![]() ≥1的”时,可得“a≥
≥1的”时,可得“a≥![]() ”
”
即“对任意的正数x,2x+![]() ≥1”?“a=
≥1”?“a=![]() ”为假命题;
”为假命题;
故“a=![]() ”是“对任意的正数x,2x+
”是“对任意的正数x,2x+![]() ≥1的”充分不必要条件
≥1的”充分不必要条件
故选A
【题型】单选题
【结束】
9
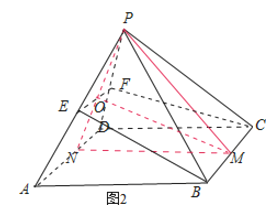
【题目】如图是一几何体的平面展开图,其中![]() 为正方形,
为正方形, ![]() ,
, ![]() 分别为
分别为![]() ,
, ![]() 的中点,在此几何体中,给出下面四个结论:①直线
的中点,在此几何体中,给出下面四个结论:①直线![]() 与直线
与直线![]() 异面;②直线
异面;②直线![]() 与直线
与直线![]() 异面;③直线
异面;③直线![]() 平面
平面![]() ;④平面
;④平面![]() 平面
平面![]() .
.
其中一定正确的选项是( )

A. ①③ B. ②③ C. ②③④ D. ①③④
参考答案:
【答案】B
【解析】 如图所示:
①连接![]() ,则
,则![]() 分别为
分别为![]() 的中点,所以
的中点,所以![]() ,所以
,所以![]() ,
,
所以![]() 共面,所以直线
共面,所以直线![]() 与
与![]() 不是异面直线,所以错误;
不是异面直线,所以错误;
②因为![]() 平面
平面![]() 平面
平面![]() 平面
平面![]() ,
,
所以直线![]() 与直线
与直线![]() 是异面直线,所以是正确的;
是异面直线,所以是正确的;
③由①知![]() ,因为
,因为![]() 平面
平面![]() 平面
平面![]() ,所以直线
,所以直线![]() 平面
平面![]() ,所以正确;
,所以正确;
④假设平面![]() 平面
平面![]() ,过点
,过点![]() 作
作![]() 分别交
分别交![]() 于点
于点![]() ,在
,在![]() 上取一点
上取一点![]() ,连接
,连接![]() ,所以
,所以![]() ,又
,又![]() ,所以
,所以![]() .
.
若![]() 时,必然平面
时,必然平面![]() 与平面
与平面![]() 不垂直,所以不正确,故选B.
不垂直,所以不正确,故选B.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设椭圆的两个焦点分别为
 ,
,  ,过
,过 作椭圆长轴的垂线交椭圆于点
作椭圆长轴的垂线交椭圆于点 ,若
,若 为等腰直角三角形,则椭圆的离心率是( )
为等腰直角三角形,则椭圆的离心率是( )A.
 B.
B.  C.
C.  D.
D. 
【答案】C
【解析】试题分析:解:设点P在x轴上方,坐标为(
 ),∵
),∵ 为等腰直角三角形,∴|PF2|=|F1F2|,
为等腰直角三角形,∴|PF2|=|F1F2|,  ,故选D.
,故选D.考点:椭圆的简单性质
点评:本题主要考查了椭圆的简单性质.椭圆的离心率是高考中选择填空题常考的题目.应熟练掌握圆锥曲线中a,b,c和e的关系
【题型】单选题
【结束】
8【题目】“
 ”是“对任意的正数
”是“对任意的正数 ,
,  ”的( )
”的( )A. 充分不必要条件 B. 必要不充分条件 C. 充要条件 D. 既不充分也不必要条件
-
科目: 来源: 题型:
查看答案和解析>>【题目】学校从参加高一年级期中考试的学生中抽出
 名学生,并统计了她们的数学成绩(成绩均为整数且满分为
名学生,并统计了她们的数学成绩(成绩均为整数且满分为 分),数学成绩分组及各组频数如下:
分),数学成绩分组及各组频数如下:
样本频率分布表:
分组
频数
频率


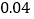















合计


(1)在给出的样本频率分布表中,求
 的值;
的值;(2)估计成绩在
 分以上(含
分以上(含 分)学生的比例;
分)学生的比例;(3)为了帮助成绩差的学生提高数学成绩,学校决定成立“二帮一”小组,即从成绩在
 的学生中选两位同学,共同帮助成绩在
的学生中选两位同学,共同帮助成绩在 中的某一位同学.已知甲同学的成绩为
中的某一位同学.已知甲同学的成绩为 分,乙同学的成绩为
分,乙同学的成绩为 分,求甲、乙两同学恰好被安排在同一小组的概率.
分,求甲、乙两同学恰好被安排在同一小组的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某公园摩天轮的半径为
 ,圆心距地面的高度为
,圆心距地面的高度为 ,摩天轮做匀速转动,每
,摩天轮做匀速转动,每 转一圈,摩天轮上的点
转一圈,摩天轮上的点 的起始位置在最低点处.
的起始位置在最低点处.(1)已知在时刻
 时
时 距离地面的高度
距离地面的高度 ,(其中
,(其中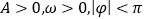 ),求
),求 时
时 距离地面的高度;
距离地面的高度;(2)当离地面
 以上时,可以看到公园的全貌,求转一圈中有多少时间可以看到公园的全貌?
以上时,可以看到公园的全貌,求转一圈中有多少时间可以看到公园的全貌?
-
科目: 来源: 题型:
查看答案和解析>>【题目】设
 为双曲线
为双曲线 :
:  的右焦点,过坐标原点的直线依次与双曲线
的右焦点,过坐标原点的直线依次与双曲线 的左、右支交于点
的左、右支交于点 ,若
,若 ,
,  ,则该双曲线的离心率为( )
,则该双曲线的离心率为( )A.
 B.
B.  C.
C.  D.
D. 
【答案】B
【解析】
 ,设双曲线的左焦点为
,设双曲线的左焦点为 ,连接
,连接 ,由对称性可知,
,由对称性可知,  为矩形,且
为矩形,且 ,故
,故 ,故选B.
,故选B.【 方法点睛】本题主要考查双曲线的定义及离心率,属于难题.离心率的求解在圆锥曲线的考查中是一个重点也是难点,一般求离心率有以下几种情况:①直接求出
 ,从而求出
,从而求出 ;②构造
;②构造 的齐次式,求出
的齐次式,求出 ;③采用离心率的定义以及圆锥曲线的定义来求解;④根据圆锥曲线的统一定义求解.
;③采用离心率的定义以及圆锥曲线的定义来求解;④根据圆锥曲线的统一定义求解.【题型】单选题
【结束】
12【题目】点
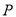 到点
到点 ,
,  及到直线
及到直线 的距离都相,如果这样的点恰好只有一个,那么实数
的距离都相,如果这样的点恰好只有一个,那么实数 的值是( )
的值是( )A.
 B.
B.  C.
C.  或
或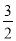 D.
D.  或
或
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知向量
 ,函数
,函数 的最小值为
的最小值为 .
.(1)当
 时,求
时,求 的值;
的值;(2)求
 ;
;(3)已知函数
 为定义在上的增函数,且对任意的
为定义在上的增函数,且对任意的 都满足
都满足 ,问:是否存在这样的实数
,问:是否存在这样的实数 ,使不等式
,使不等式 对所有
对所有 恒成立,若存在,求出
恒成立,若存在,求出 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】某几何体的三视图如图所示,且该几何体的体积是3,则正视图的
 的值__________.
的值__________.
【答案】3
【解析】 由已知中的三视图可得该几何体是一个以直角梯形为底面,梯形上下边长为
 和
和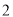 ,高为
,高为 ,
,如图所示,
 平面
平面 ,
,所以底面积为
 ,
,几何体的高为
 ,所以其体积为
,所以其体积为 .
.
点睛:在由三视图还原为空间几何体的实际形状时,要从三个视图综合考虑,根据三视图的规则,空间几何体的可见轮廓线在三视图中为实线,不可见轮廓线在三视图中为虚线.在还原空间几何体实际形状时,一般是以正视图和俯视图为主,结合侧视图进行综合考虑.求解以三视图为载体的空间几何体的体积的关键是由三视图确定直观图的形状以及直观图中线面的位置关系和数量关系,利用相应体积公式求解.
【题型】填空题
【结束】
16【题目】已知椭圆
 :
:  的右焦点为
的右焦点为 ,
,  为直线
为直线 上一点,线段
上一点,线段 交
交 于点
于点 ,若
,若 ,则
,则 __________.
__________.
相关试题

