【题目】如图,某公园摩天轮的半径为![]() ,圆心距地面的高度为
,圆心距地面的高度为![]() ,摩天轮做匀速转动,每
,摩天轮做匀速转动,每![]() 转一圈,摩天轮上的点
转一圈,摩天轮上的点![]() 的起始位置在最低点处.
的起始位置在最低点处.
(1)已知在时刻![]() 时
时![]() 距离地面的高度
距离地面的高度![]() ,(其中
,(其中![]() ),求
),求![]() 时
时![]() 距离地面的高度;
距离地面的高度;
(2)当离地面![]() 以上时,可以看到公园的全貌,求转一圈中有多少时间可以看到公园的全貌?
以上时,可以看到公园的全貌,求转一圈中有多少时间可以看到公园的全貌?

参考答案:
【答案】(1)70;(2)转一圈中有![]() 钟时间可以看到公园全貌.
钟时间可以看到公园全貌.
【解析】分析:(1)由实际问题求出三角函数中的参数![]() ,
,![]() ,及周期
,及周期![]() ,利用三角函数的周期公式求出
,利用三角函数的周期公式求出![]() ,通过初始位置求出
,通过初始位置求出![]() ,求出
,求出![]() ,将
,将![]() 用2017代替求出2017min时点P距离地面的高度;
用2017代替求出2017min时点P距离地面的高度;
(2)由(1)知![]() ,
,
依题意,![]() ,求出
,求出![]() 的范围,即可求得转一圈中有
的范围,即可求得转一圈中有![]() 钟时间可以看到公园全貌.
钟时间可以看到公园全貌.
详解:
(1)依题意,![]() ,则
,则![]() ,
,
且![]() ,
,
故![]() ,
,
∴![]()
∴![]()
(2)由(1)知![]() ,
,
依题意,![]() ,
,
∴![]()
![]()
∵![]() ,
,
∴转一圈中有![]() 钟时间可以看到公园全貌.
钟时间可以看到公园全貌.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆
 ,直线
,直线 。
。(Ⅰ)求证:直线
 与圆C恒有两个交点;
与圆C恒有两个交点;(Ⅱ)求出直线
 被圆C截得的最短弦长,并求出截得最短弦长时的
被圆C截得的最短弦长,并求出截得最短弦长时的 的值;
的值;(Ⅲ)设直线
 与圆C的两个交点为M,N,且
与圆C的两个交点为M,N,且 (点C为圆C的圆心),求直线
(点C为圆C的圆心),求直线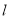 的方程。
的方程。 -
科目: 来源: 题型:
查看答案和解析>>【题目】设椭圆的两个焦点分别为
 ,
,  ,过
,过 作椭圆长轴的垂线交椭圆于点
作椭圆长轴的垂线交椭圆于点 ,若
,若 为等腰直角三角形,则椭圆的离心率是( )
为等腰直角三角形,则椭圆的离心率是( )A.
 B.
B.  C.
C.  D.
D. 
【答案】C
【解析】试题分析:解:设点P在x轴上方,坐标为(
 ),∵
),∵ 为等腰直角三角形,∴|PF2|=|F1F2|,
为等腰直角三角形,∴|PF2|=|F1F2|,  ,故选D.
,故选D.考点:椭圆的简单性质
点评:本题主要考查了椭圆的简单性质.椭圆的离心率是高考中选择填空题常考的题目.应熟练掌握圆锥曲线中a,b,c和e的关系
【题型】单选题
【结束】
8【题目】“
 ”是“对任意的正数
”是“对任意的正数 ,
,  ”的( )
”的( )A. 充分不必要条件 B. 必要不充分条件 C. 充要条件 D. 既不充分也不必要条件
-
科目: 来源: 题型:
查看答案和解析>>【题目】学校从参加高一年级期中考试的学生中抽出
 名学生,并统计了她们的数学成绩(成绩均为整数且满分为
名学生,并统计了她们的数学成绩(成绩均为整数且满分为 分),数学成绩分组及各组频数如下:
分),数学成绩分组及各组频数如下:
样本频率分布表:
分组
频数
频率


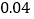















合计


(1)在给出的样本频率分布表中,求
 的值;
的值;(2)估计成绩在
 分以上(含
分以上(含 分)学生的比例;
分)学生的比例;(3)为了帮助成绩差的学生提高数学成绩,学校决定成立“二帮一”小组,即从成绩在
 的学生中选两位同学,共同帮助成绩在
的学生中选两位同学,共同帮助成绩在 中的某一位同学.已知甲同学的成绩为
中的某一位同学.已知甲同学的成绩为 分,乙同学的成绩为
分,乙同学的成绩为 分,求甲、乙两同学恰好被安排在同一小组的概率.
分,求甲、乙两同学恰好被安排在同一小组的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】“
 ”是“对任意的正数
”是“对任意的正数 ,
,  ”的( )
”的( )A. 充分不必要条件 B. 必要不充分条件 C. 充要条件 D. 既不充分也不必要条件
【答案】A
【解析】分析:根据基本不等式,我们可以判断出“
 ”?“对任意的正数x,2x+
”?“对任意的正数x,2x+ ≥1”与“对任意的正数x,2x+
≥1”与“对任意的正数x,2x+ ≥1”?“a=
≥1”?“a=”真假,进而根据充要条件的定义,即可得到结论.
解答:解:当“a=
 ”时,由基本不等式可得:
”时,由基本不等式可得:“对任意的正数x,2x+
 ≥1”一定成立,
≥1”一定成立,即“a=
 ”?“对任意的正数x,2x+
”?“对任意的正数x,2x+ ≥1”为真命题;
≥1”为真命题;而“对任意的正数x,2x+
 ≥1的”时,可得“a≥
≥1的”时,可得“a≥ ”
”即“对任意的正数x,2x+
 ≥1”?“a=
≥1”?“a= ”为假命题;
”为假命题;故“a=
 ”是“对任意的正数x,2x+
”是“对任意的正数x,2x+ ≥1的”充分不必要条件
≥1的”充分不必要条件故选A
【题型】单选题
【结束】
9【题目】如图是一几何体的平面展开图,其中
 为正方形,
为正方形,  ,
,  分别为
分别为 ,
,  的中点,在此几何体中,给出下面四个结论:①直线
的中点,在此几何体中,给出下面四个结论:①直线 与直线
与直线 异面;②直线
异面;②直线 与直线
与直线 异面;③直线
异面;③直线 平面
平面 ;④平面
;④平面 平面
平面 .
.其中一定正确的选项是( )

A. ①③ B. ②③ C. ②③④ D. ①③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】设
 为双曲线
为双曲线 :
:  的右焦点,过坐标原点的直线依次与双曲线
的右焦点,过坐标原点的直线依次与双曲线 的左、右支交于点
的左、右支交于点 ,若
,若 ,
,  ,则该双曲线的离心率为( )
,则该双曲线的离心率为( )A.
 B.
B.  C.
C.  D.
D. 
【答案】B
【解析】
 ,设双曲线的左焦点为
,设双曲线的左焦点为 ,连接
,连接 ,由对称性可知,
,由对称性可知,  为矩形,且
为矩形,且 ,故
,故 ,故选B.
,故选B.【 方法点睛】本题主要考查双曲线的定义及离心率,属于难题.离心率的求解在圆锥曲线的考查中是一个重点也是难点,一般求离心率有以下几种情况:①直接求出
 ,从而求出
,从而求出 ;②构造
;②构造 的齐次式,求出
的齐次式,求出 ;③采用离心率的定义以及圆锥曲线的定义来求解;④根据圆锥曲线的统一定义求解.
;③采用离心率的定义以及圆锥曲线的定义来求解;④根据圆锥曲线的统一定义求解.【题型】单选题
【结束】
12【题目】点
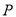 到点
到点 ,
,  及到直线
及到直线 的距离都相,如果这样的点恰好只有一个,那么实数
的距离都相,如果这样的点恰好只有一个,那么实数 的值是( )
的值是( )A.
 B.
B.  C.
C.  或
或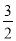 D.
D.  或
或
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知向量
 ,函数
,函数 的最小值为
的最小值为 .
.(1)当
 时,求
时,求 的值;
的值;(2)求
 ;
;(3)已知函数
 为定义在上的增函数,且对任意的
为定义在上的增函数,且对任意的 都满足
都满足 ,问:是否存在这样的实数
,问:是否存在这样的实数 ,使不等式
,使不等式 对所有
对所有 恒成立,若存在,求出
恒成立,若存在,求出 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.
相关试题

