【题目】已知函数![]()
(I)求函数![]() 在
在![]() 上的最小值;
上的最小值;
(II)若函数![]() 与
与![]() 的图象恰有一个公共点,求实数
的图象恰有一个公共点,求实数![]() 的值.
的值.
参考答案:
【答案】(1)见解析(2)3
【解析】试题分析:(1)先求函数导数,根据导函数零点![]() 与定义区间
与定义区间![]() 位置关系讨论最值取法:当
位置关系讨论最值取法:当![]() 时,最小值为
时,最小值为![]() ,当
,当![]() 时,最小值为
时,最小值为![]() ,
,
(2)先将公共点转化为对应方程的解: ![]() 在
在![]() 上有且只有一个根.利用导数研究函数
上有且只有一个根.利用导数研究函数![]() 单调性:先将后增,确定有且只有一个根充要条件:
单调性:先将后增,确定有且只有一个根充要条件: ![]() .
.
试题解析:(I)令![]() ,得
,得![]() .
.
①当![]() 时,函数
时,函数![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
此时函数![]() 在区间
在区间![]() 上的最小值为
上的最小值为![]()
②当![]() 时,函数
时,函数![]() 在区间
在区间![]() 上单调递增,此时函数
上单调递增,此时函数![]() 在区间
在区间![]() 上的最小值为
上的最小值为![]()
(II)由题意得, ![]() 在
在![]() 上有且只有一个根,
上有且只有一个根,
即![]() 在
在![]() 上有且只有一个根. 令
上有且只有一个根. 令![]() ,
,
则![]() ,
,
易知![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,所以
上单调递增,所以![]() ,
,
由题意可知,若使![]() 与
与![]() 的图象恰有一个公共点,则
的图象恰有一个公共点,则![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】设
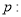 方程
方程 有两个不等的负根,
有两个不等的负根, 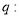 方程
方程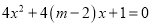 无实根,若“
无实根,若“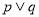 ”为真,“
”为真,“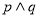 ”为假,求实数
”为假,求实数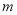 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】设关于x的一元二次方程x2+2ax+b2=0.
(1)若a是从0,1,2,3四个数中任取的一个数,b是从0,1,2三个数中任取的一个数,求上述方程有实根的概率.
(2)若a是从区间[0,3]任取的一个数,b是从区间[0,2]任取的一个数,求上述方程有实根的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 ,
,  ,
,  .
.(1)当
 时,试比较
时,试比较 与
与 的大小关系;
的大小关系;(2)猜想
 与
与 的大小关系,并给出证明.
的大小关系,并给出证明. -
科目: 来源: 题型:
查看答案和解析>>【题目】设样本x1,x2,…,x10数据的平均值和方差分别为3和5,若yi=xi+a(a为非零实数,i=1,2,…,10),则y1,y2,…,y10的均值和方差分别为( )
A. 3,5 B. 3+a,5 C. 3+a,5+a D. 3,5+a
-
科目: 来源: 题型:
查看答案和解析>>【题目】某同学在研究性学习中,关于三角形与三角函数知识的应用(约定三内角
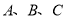 所对的边分别是
所对的边分别是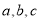 )得出如下一些结论:
)得出如下一些结论:(1)若
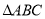 是钝角三角形,则
是钝角三角形,则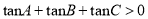 ;
;(2)若
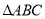 是锐角三角形,则
是锐角三角形,则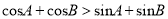 ;
;(3)在三角形
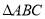 中,若
中,若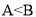 ,则
,则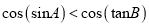
(4)在
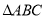 中,若
中,若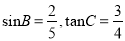 ,则
,则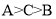
其中错误命题的个数是 ( )
A. 0 B. 1 C. 2 D. 3
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于无穷数列
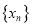 和函数
和函数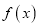 ,若
,若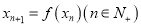 ,则称
,则称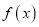 是数列
是数列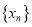 的母函数.
的母函数.(Ⅰ)定义在
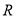 上的函数
上的函数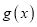 满足:对任意
满足:对任意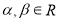 ,都有
,都有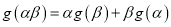 ,且
,且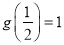 ;又数列
;又数列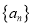 满足
满足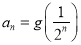 .
. (1)求证:
 是数列
是数列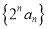 的母函数;
的母函数;(2)求数列
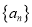 的前项
的前项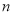 和
和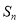 .
.(Ⅱ)已知
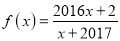 是数列
是数列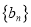 的母函数,且
的母函数,且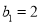 .若数列
.若数列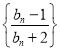 的前
的前 项和为
项和为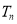 ,求证:
,求证: 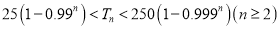 .
.
相关试题

