【题目】已知点![]() 及圆
及圆![]() .
.
(1)若直线![]() 过点
过点![]() 且与圆心
且与圆心![]() 的距离为1,求直线
的距离为1,求直线![]() 的方程;
的方程;
(2)设过点![]() 的直线
的直线![]() 与圆
与圆![]() 交于
交于![]() 两点,当
两点,当![]() 时,求以线段
时,求以线段![]() 为直径的圆
为直径的圆![]() 的方程;
的方程;
(3)设直线![]() 与圆
与圆![]() 交于
交于![]() 两点,是否存在实数
两点,是否存在实数![]() ,使得过点
,使得过点![]() 的直线
的直线![]() 垂直平分弦
垂直平分弦![]() ?若存在,求出实数
?若存在,求出实数![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
参考答案:
【答案】(1)![]() 或
或![]() ;(2)
;(2)![]() ;(3)不存在.
;(3)不存在.
【解析】
(1)设出直线方程,结合点到直线距离公式,计算参数,即可。(2)证明得到点P为MN的中点,建立圆方程,即可。(3)将直线方程代入圆方程,结合交点个数,计算a的范围,计算直线![]() 的斜率,计算a的值,即可。
的斜率,计算a的值,即可。
(1)直线![]() 斜率存在时,设直线
斜率存在时,设直线![]() 的斜率为
的斜率为![]() ,则方程为
,则方程为![]() ,即
,即![]() .又圆
.又圆![]() 的圆心为
的圆心为![]() ,半径
,半径![]() ,由
,由![]() ,解得
,解得![]() .
.
所以直线方程为![]() ,即
,即![]() .
.
当![]() 的斜率不存在时,
的斜率不存在时,![]() 的方程为
的方程为![]() ,经验证
,经验证![]() 也满足条件.
也满足条件.
即直线![]() 的方程为
的方程为![]() 或
或![]() .
.
(2)由于![]() ,而弦心距
,而弦心距![]() ,
,
所以![]() .
.
所以![]() 恰为
恰为![]() 的中点.
的中点.
故以![]() 为直径的圆
为直径的圆![]() 的方程为
的方程为![]() .
.
(3)把直线![]() 代入圆
代入圆![]() 的方程,消去
的方程,消去![]() ,整理得
,整理得![]() .
.
由于直线![]() 交圆
交圆![]() 于
于![]() 两点,
两点,
故![]() ,
,
即![]() ,解得
,解得![]() .
.
则实数![]() 的取值范围是
的取值范围是![]() .
.
设符合条件的实数![]() 存在,
存在,
由于![]() 垂直平分弦
垂直平分弦![]() ,故圆心
,故圆心![]()
![]() 必在
必在![]() 上.所以
上.所以![]() 的斜率
的斜率![]() ,
,
而![]() ,
,
所以![]() .由于
.由于![]()
![]() ,
,
故不存在实数![]() ,使得过点
,使得过点![]() 的直线
的直线![]() 垂直平分弦
垂直平分弦![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列关于回归分析的说法中错误的有( )个
(1). 残差图中残差点所在的水平带状区域越宽,则回归方程的预报精确度越高.
(2). 回归直线一定过样本中心
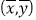 。
。(3). 两个模型中残差平方和越小的模型拟合的效果越好。
(4) .甲、乙两个模型的
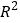 分别约为0.88和0.80,则模型乙的拟合效果更好.
分别约为0.88和0.80,则模型乙的拟合效果更好.A. 4 B. 3 C. 2 D. 1
-
科目: 来源: 题型:
查看答案和解析>>【题目】有一圆与直线
 相切于点
相切于点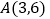 ,且经过点
,且经过点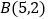 ,求此圆的方程.
,求此圆的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】正方形
 和四边形
和四边形 所在的平面互相垂直,
所在的平面互相垂直, ,
, ,
, .
.求证:(1)
 平面
平面 ;
;(2)
 平面
平面 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆C的圆心C在直线
 上.
上. 若圆C与y轴的负半轴相切,且该圆截x轴所得的弦长为
若圆C与y轴的负半轴相切,且该圆截x轴所得的弦长为 ,求圆C的标准方程;
,求圆C的标准方程; 已知点
已知点 ,圆C的半径为3,且圆心C在第一象限,若圆C上存在点M,使
,圆C的半径为3,且圆心C在第一象限,若圆C上存在点M,使 为坐标原点
为坐标原点 ,求圆心C的纵坐标的取值范围.
,求圆心C的纵坐标的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列推理过程不是演绎推理的是( ).
①一切奇数都不能被2整除,2019是奇数, 2019不能被2整除;
②由“正方形面积为边长的平方”得到结论:正方体的体积为棱长的立方;
③在数列
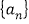 中,
中,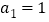 ,
,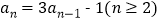 ,由此归纳出
,由此归纳出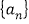 的通项公式;
的通项公式;④由“三角形内角和为
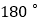 ”得到结论:直角三角形内角和为
”得到结论:直角三角形内角和为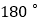 .
.A. ① ② B. ② ③ C. ③ ④ D. ②④
-
科目: 来源: 题型:
查看答案和解析>>【题目】2018年10月24日,世界上最长的跨海大桥一港珠澳大桥正式通车
 在一般情况下,大桥上的车流速度
在一般情况下,大桥上的车流速度 单位:千米
单位:千米 时
时 是车流密度
是车流密度 单位:辆
单位:辆 千米
千米 的函数
的函数 当桥上的车流密度达到220辆
当桥上的车流密度达到220辆 千米时,将造成堵塞,此时车流速度为0;当车流密度不超过20辆
千米时,将造成堵塞,此时车流速度为0;当车流密度不超过20辆 千米时,车流速度为100千米
千米时,车流速度为100千米 时,研究表明:当
时,研究表明:当 时,车流速度v是车流密度x的一次函数.
时,车流速度v是车流密度x的一次函数. Ⅰ
Ⅰ 当
当 时,求函数
时,求函数 的表达式;
的表达式; Ⅱ
Ⅱ 当车流密度x为多大时,车流量
当车流密度x为多大时,车流量 单位时间内通过桥上某观测点的车辆数,单位:辆
单位时间内通过桥上某观测点的车辆数,单位:辆 时
时 可以达到最大?并求出最大值.
可以达到最大?并求出最大值.
相关试题

