【题目】(1)由0,1,2,…,9这十个数字组成的无重复数字的四位数中,十位数字与千位数字之差的绝对值等于7的四位数的个数共有几种?
(2)我校高三学习雷锋志愿小组共有16人,其中一班、二班、三班、四班各4人,现在从中任选3人,要求这三人不能是同一个班级的学生,且在三班至多选1人,求不同的选取法的种数.
参考答案:
【答案】(1)280种;(2)472种.
【解析】
(1)千位数字和十位数字的组合有![]() 五种,百位和个位的数共有
五种,百位和个位的数共有![]() 种组合,计算得到答案.
种组合,计算得到答案.
(2)考虑不选三班的同学和选三班的一位同学两种情况,利用排除法和分步分类计数原理得到答案.
(1)十位数字与千位数字之差的绝对值等于7,
可得千位数字和十位数字的组合有![]() 五种,
五种,
每种组合中百位和个位的数共有![]() 种组合,所以符合条件的四位数共有
种组合,所以符合条件的四位数共有![]() 种.
种.
(2)情形一:不选三班的同学,从12个人中选出3人,有![]() 种选取方法,其中来自同一个班级的情况有
种选取方法,其中来自同一个班级的情况有![]() 种,则此时有
种,则此时有![]() 种选取方法;
种选取方法;
情形二:选三班的一位同学,三班的这一位同学的选取方法有4种,剩下的两位同学从剩下的12人中任选2人,有![]() 种选取方法,则此时有
种选取方法,则此时有![]() 种选取方法.
种选取方法.
根据分类计数原理,共有![]() 种选取方法.
种选取方法.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系
 中,曲线
中,曲线 与坐标轴的交点都在圆
与坐标轴的交点都在圆 上.
上.(1)求圆
 的方程;
的方程;(2)若圆
 与直线
与直线 交于
交于 ,
, 两点,且
两点,且 ,求
,求 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某公司生产一种产品,每年投入固定成本0.5万元,此外每生产100件这种产品还需要增加投资0.25万元,经预测可知,市场对这种产品的年需求量为500件,当出售的这种产品的数量为t(单位:百件)时,销售所得的收入约为
 (万元).
(万元).(1)若该公司的年产量为x(单位:百件),试把该公司生产并销售这种产品所得的年利润表示为年产量x的函数;
(2)当这种产品的年产量为多少时,当年所得利润最大?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 ,求证:
,求证: .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
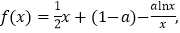 ,其中
,其中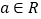 .
.(1)试讨论函数
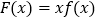 的单调性;
的单调性;(2)若
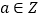 ,且函数
,且函数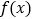 有两个零点,求实数
有两个零点,求实数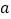 的最小值.
的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】超市为了防止转基因产品影响民众的身体健康,要求产品在进入超市前必须进行两轮转基因检测,只有两轮都合格才能销售,否则不能销售.已知某产品第一轮检测不合格的概率为
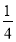 ,第二轮检测不合格的概率为
,第二轮检测不合格的概率为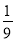 ,两轮检测是否合格相互没有影响.
,两轮检测是否合格相互没有影响.(1)求该产品不能销售的概率;
(2)如果产品可以销售,则每件产品可获利50元;如果产品不能销售,则每件产品亏损60元.已知一箱中有产品4件,记一箱产品获利
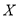 元,求
元,求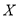 的分布列,并求出均值
的分布列,并求出均值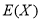 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】某林场现有木材存量为
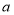 ,每年以25%的增长率逐年递增,但每年年底要砍伐的木材量为
,每年以25%的增长率逐年递增,但每年年底要砍伐的木材量为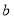 ,经过
,经过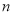 年后林场木材存有量为
年后林场木材存有量为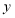
(1)求
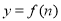 的解析式
的解析式(2)为保护生态环境,防止水土流失,该地区每年的森林木材存量不应少于
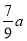 ,如果
,如果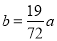 ,那么该地区会发生水土流失吗?若会,要经过几年?(取
,那么该地区会发生水土流失吗?若会,要经过几年?(取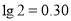 )
)
相关试题

