【题目】已知Sn为数列{an}的前n项和,an>0,an2+2an=4Sn﹣1.
(1)求{an}的通项公式;
(2)设bn= ![]() ,求{bn}的前n项和Tn .
,求{bn}的前n项和Tn .
(3)cn= ![]() ,{cn}的前n项和为Dn , 求证:Dn<
,{cn}的前n项和为Dn , 求证:Dn< ![]() .
.
参考答案:
【答案】
(1)解:当n=1时, ![]() ,解之得a1=1;
,解之得a1=1;
当n≥2时 ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,因为an>0,
,因为an>0,
所以 ![]() ,
,
所以数列{an}是以1为首项,2为公差的等差数列,所以an=2n﹣1
(2)解:∵ ![]()
∴ ![]()
(3)证明: ![]() =
= ![]()
Dn=c1+c2+c3+…+cn= ![]() =
= ![]() ,即
,即 ![]()
【解析】(1)由an2+2an=4Sn﹣1,可求得a1 , 当n≥2时,下推一项后两式作差,整理可得以 ![]() ,利用等差数列的定义可判断数列{an}为等差数列,继而可得其通项公式;(2)利用裂项法可得
,利用等差数列的定义可判断数列{an}为等差数列,继而可得其通项公式;(2)利用裂项法可得 ![]() ,累加可求{bn}的前n项和Tn . (3)利用放缩法得
,累加可求{bn}的前n项和Tn . (3)利用放缩法得 ![]() =
= ![]() ,从而可求{cn}的前n项和为Dn , 即证:Dn<
,从而可求{cn}的前n项和为Dn , 即证:Dn< ![]() .
.
【考点精析】通过灵活运用数列的前n项和和数列的通项公式,掌握数列{an}的前n项和sn与通项an的关系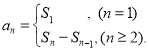 ;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式即可以解答此题.
;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个正三角形等分成4个全等的小正三角形,将中间的一个正三角形挖掉(如图1),再将剩余的每个正三角形分成4个全等的小正三角形,并将中间的一个正三角形挖掉,得图2,如此继续下去…
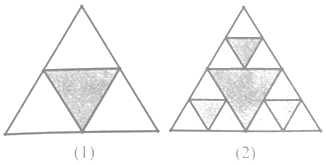
(1)图3共挖掉多少个正三角形?
(2)设原正三角形边长为a,第n个图形共挖掉多少个正三角形?这些正三角形面积和为多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,有一壁画,最高点A处离地面AO=4m,最低点B处离地面BO=2m,观赏它的C点在过墙角O点与地面成30°角的射线上.

(1)设点C到墙的距离为x,当x= m时,求tanθ的值;
m时,求tanθ的值;
(2)问C点离墙多远时,视角θ最大? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知f(x)=3x2﹣2x,数列{an}的前n项和为Sn , 点(n,Sn)(n∈N*)均在函数y=f(x)的图像上.
(1)求数列{an}的通项公式;
(2)设bn=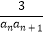 ,Tn是数列{bn}的前n项和,求使得Tn<
,Tn是数列{bn}的前n项和,求使得Tn< 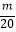 对所有n∈N*都成立的最小正整数m.
对所有n∈N*都成立的最小正整数m. -
科目: 来源: 题型:
查看答案和解析>>【题目】一个单位有职工80人,其中业务人员56人,管理人员8人,服务人员16人,为了解职工的某种情况,决定采取分层抽样的方法。抽取一个容量为10的样本,每个管理人员被抽到的概率为( )
A.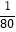
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】有甲、乙两个粮食经销商每次在同一粮食生产地以相同的价格购进粮食,他们共购进粮食两次,各次的粮食价格不同,甲每次购粮10000千克,乙每次购粮食10000元,在两次统计中,购粮的平均价格较低的是( )
A.甲
B.乙
C.一样低
D.不确定 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知等比数列{an}的前n项和Sn=2n+r.
(1)求实数r的值和{an}的通项公式;
(2)若数列{bn}满足b1=1,bn+1﹣bn=log2an+1 , 求bn .
相关试题

