【题目】现有4人去旅游,旅游地点有A,B两个地方可以选择,但4人都不知道去哪里玩,于是决定通过掷一枚质地均匀的骰子决定自己去哪里玩,掷出能被3整除的数时去A地,掷出其他的则去B地.
(1)求这4个人恰好有1个人去A地的概率;
(2)用X,Y分别表示这4个人中去A,B两地的人数,记ξ=XY,求随机变量ξ的分布列与数学期望E(ξ).
参考答案:
【答案】
(1)解:由题意这4人中,每个人去A地旅游的概率为 ![]() ,去B地旅游的概率为
,去B地旅游的概率为 ![]() ,
,
设“这4个人中恰有i人去A地旅游”为事件Ai(i=0,1,2,3,4),
∴P(Ai)= ![]() ,
,
∴这4个人恰好有1个人去A地的概率:
P(A1)= ![]() =
= ![]()
(2)解:由题意ξ的可能取值为0,3,4,
P(ξ=0)=P(A0)+P(A4)= ![]() =
= ![]() ,
,
P(ξ=3)=P(A1)+P(A3)= ![]() +
+ ![]() =
= ![]() ,
,
P(ξ=4)=P(A2)= ![]() ═
═ ![]() ,
,
∴ξ的分布列为:
ξ | 0 | 3 | 4 |
P |
|
|
|
Eξ= ![]() =
= ![]()
【解析】(1)由题意这4人中,每个人去A地旅游的概率为 ![]() ,去B地旅游的概率为
,去B地旅游的概率为 ![]() ,设“这4个人中恰有i人去A地旅游”为事件Ai(i=0,1,2,3,4),P(Ai)=
,设“这4个人中恰有i人去A地旅游”为事件Ai(i=0,1,2,3,4),P(Ai)= ![]() ,由此能求出这4个人恰好有1个人去A地的概率.(2)由题意ξ的可能取值为0,3,4,分别求出相应的概率,由此能求出随机变量ξ的分布列与数学期望E(ξ).
,由此能求出这4个人恰好有1个人去A地的概率.(2)由题意ξ的可能取值为0,3,4,分别求出相应的概率,由此能求出随机变量ξ的分布列与数学期望E(ξ).
【考点精析】通过灵活运用离散型随机变量及其分布列,掌握在射击、产品检验等例子中,对于随机变量X可能取的值,我们可以按一定次序一一列出,这样的随机变量叫做离散型随机变量.离散型随机变量的分布列:一般的,设离散型随机变量X可能取的值为x1,x2,.....,xi,......,xn,X取每一个值 xi(i=1,2,......)的概率P(ξ=xi)=Pi,则称表为离散型随机变量X 的概率分布,简称分布列即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】十九大指出中国的电动汽车革命早已展开,通过以新能源汽车替代汽/柴油车,中国正在大力实施一项将重塑全球汽车行业的计划.
 年某企业计划引进新能源汽车生产设备,通过市场分析,全年需投入固定成本
年某企业计划引进新能源汽车生产设备,通过市场分析,全年需投入固定成本 万元,每生产
万元,每生产 (百辆),需另投入成本
(百辆),需另投入成本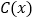 万元,且
万元,且 .由市场调研知,每辆车售价
.由市场调研知,每辆车售价 万元,且全年内生产的车辆当年能全部销售完.
万元,且全年内生产的车辆当年能全部销售完.(1)求出2018年的利润
 (万元)关于年产量
(万元)关于年产量 (百辆)的函数关系式;(利润=销售额-成本)
(百辆)的函数关系式;(利润=销售额-成本)(2)2018年产量为多少百辆时,企业所获利润最大?并求出最大利润.
-
科目: 来源: 题型:
查看答案和解析>>【题目】供电部门对某社区1000位居民2017年12月份人均用电情况进行统计后,按人均用电量分为
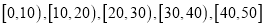 五组,整理得到如下的频率分布直方图,则下列说法错误的是( )
五组,整理得到如下的频率分布直方图,则下列说法错误的是( )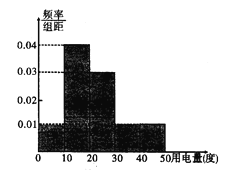
A. 12月份人均用电量人数最多的一组有400人
B. 12月份人均用电量不低于20度的有500人
C. 12月份人均用电量为25度
D. 在这1000位居民中任选1位协助收费,选到的居民用电量在
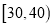 —组的概率为
—组的概率为
-
科目: 来源: 题型:
查看答案和解析>>【题目】从一堆产品
 正品与次品都多于2件
正品与次品都多于2件 中任取2件,观察正品件数和次品件数,则下列说法:
中任取2件,观察正品件数和次品件数,则下列说法: “恰好有1件次品”和“恰好2件都是次品”是互斥事件
“恰好有1件次品”和“恰好2件都是次品”是互斥事件 “至少有1件正品”和“全是次品”是对立事件
“至少有1件正品”和“全是次品”是对立事件 “至少有1件正品”和“至少有1件次品”是互斥事件但不是对立事件
“至少有1件正品”和“至少有1件次品”是互斥事件但不是对立事件 “至少有1件次品”和“全是正品”是互斥事件也是对立事件
“至少有1件次品”和“全是正品”是互斥事件也是对立事件其中正确的有______
 填序号
填序号 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】某企业生产甲、乙两种产品,已知生产每吨甲产品要用A原料3吨,B原料2吨,生产每吨乙产品要用A原料1吨,B原料3吨。销售每吨甲产品可获得利润5万元,每吨乙产品可获得利润3万元,该企业在一个生产周期内消耗A原料不超过13吨,B原料不超过18吨,那么该企业可获得最大利润是___________万元
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在四棱柱ABCD﹣A1B1C1D1中,底面ABCD是梯形,AD∥BC,侧面ABB1A1为菱形,∠DAB=∠DAA1 .

(1)求证:A1B⊥AD;
(2)若AD=AB=2BC,∠A1AB=60°,点D在平面ABB1A1上的射影恰为线段A1B的中点,求平面DCC1D1与平面ABB1A1所成锐二面角的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某兴趣小组欲研究昼夜温差大小与患感冒人数多少之间的关系,他们分别到气象局与某医院抄录了 1至6月份每月10号的昼夜温差情况与因患感冒而就诊的人数,得到如下资料:
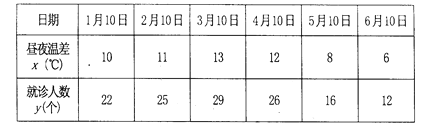
该兴趣小组确定的研究方案是:先用2、3、4、5月的4组数据求线性回归方程,再用1月和6月的2组数据进行检验.
(1)请根据2、3、4、5月的数据,求出
 关于
关于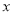 的线性回归方程
的线性回归方程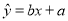 ;
;(2)若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2人,则认为得到的线性回归方程是理想的,试问该小组所得线性回归方程是否理想?
(参考公式:
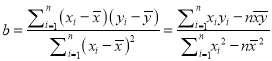 ,
, 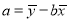 )
)参考数据:
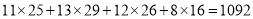 ,
, 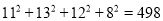 .
.
相关试题

