【题目】在直角坐标系![]() 中,以原点为极点,
中,以原点为极点, ![]() 轴的非负半轴为极轴建立极坐标系,已知直线
轴的非负半轴为极轴建立极坐标系,已知直线![]() 的参数方程为
的参数方程为 (
(![]() 为参数),曲线
为参数),曲线![]() 的极坐标方程为
的极坐标方程为![]() ,直线
,直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() .
.
(1)求直线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)求![]() 的值.
的值.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() 。
。
【解析】【试题分析】(1)分别运用代入消元法消去参数和极坐标与直角坐标之间的互化公式求解;(2)将直线![]() 的参数方程
的参数方程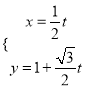 (
(![]() 为参数)代入曲线
为参数)代入曲线![]() 的直角坐标方程
的直角坐标方程![]() 可得
可得![]() ,依据参数的几何意义直接求解:
,依据参数的几何意义直接求解:
解:(1)消去参数![]() ,把直线
,把直线![]() 的参数方程
的参数方程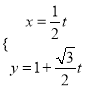 (
(![]() 为参数)化为普通方程得
为参数)化为普通方程得![]() ,
,
曲线![]() 的极坐标方程
的极坐标方程![]() 可化为
可化为![]() ,
,
∴曲线![]() 的直角坐标方程是
的直角坐标方程是![]() ,
,
即![]() .
.
(2)∵直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,
,
把直线![]() 的参数方程
的参数方程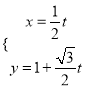 (
(![]() 为参数)代入曲线
为参数)代入曲线![]() 的直角坐标方程
的直角坐标方程![]() ,
,
得![]() ,
,
∴![]() .
.
依据参数![]() 的几何意义得
的几何意义得![]()
![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,定圆C半径为2,A为圆C上的一个定点,B为圆C上的动点,若点A,B,C不共线,且|
 |
| 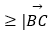 |对任意t∈(0,+∞)恒成立,则
|对任意t∈(0,+∞)恒成立,则 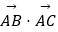 = .
= . 
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a,b∈R,若a2+b2﹣ab=1,则ab的取值范围是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】我国上是世界严重缺水的国家,城市缺水问题较为突出,某市政府为了鼓励居民节约用水,计划在本市试行居民生活用水定额管理,即确定一个合理的居民月用水量标准
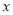 (吨),用水量不超过
(吨),用水量不超过 的部分按平价收费,超过
的部分按平价收费,超过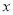 的部分按议价收费,为了了解全市民月用水量的分布情况,通过抽样,获得了100位居民某年的月用水量(单位:吨),将数据按照
的部分按议价收费,为了了解全市民月用水量的分布情况,通过抽样,获得了100位居民某年的月用水量(单位:吨),将数据按照 ,
,  ,…,
,…,  分成9组,制成了如图所示的频率分布直方图.
分成9组,制成了如图所示的频率分布直方图.
(Ⅰ)求直方图中
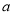 的值;
的值;(Ⅱ)已知该市有80万居民,估计全市居民中月均用水量不低于3吨的人数,并说明理由;
(Ⅲ)若该市政府希望使
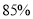 的居民每月的用水量不超过标准
的居民每月的用水量不超过标准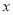 (吨),估计
(吨),估计 的值,并说明理由;
的值,并说明理由; -
科目: 来源: 题型:
查看答案和解析>>【题目】某篮球运动员在一个赛季的40场比赛中的得分的茎叶图如图所示:则中位数与众数分别为( )

A.3与3
B.23与3
C.3与23
D.23与23 -
科目: 来源: 题型:
查看答案和解析>>【题目】椭圆
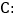
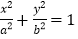 (
(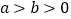 )的离心率为
)的离心率为 ,其左焦点到点
,其左焦点到点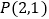 的距离为
的距离为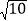 .
.(1)求椭圆
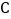 的标准方程;
的标准方程;(2)若直线
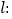
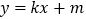 与椭圆
与椭圆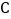 相交于
相交于 、
、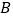 两点(
两点( 、
、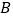 不是左右顶点),且以
不是左右顶点),且以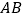 为直径的圆过椭圆
为直径的圆过椭圆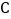 的右顶点,求证:直线
的右顶点,求证:直线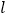 过定点,并求出该定点的坐标.
过定点,并求出该定点的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】某单位共有老、中、青职工430人,其中青年职工160人,中年职工人数是老年职工人数的2倍.为了解职工身体状况,现采用分层抽样方法进行调查,在抽取的样本中有青年职工32人,则该样本中的老年职工人数为( )
A.9
B.18
C.27
D.36
相关试题

