【题目】选修4-4:坐标系与参数方程
已知曲线![]() 的极坐标方程是
的极坐标方程是![]() ,以极点为原点,极轴为
,以极点为原点,极轴为![]() 轴的正半轴建立平面直角坐标系,直线
轴的正半轴建立平面直角坐标系,直线![]() 的参数方程为
的参数方程为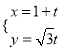 (
(![]() 为参数).
为参数).
(Ⅰ)写出直线![]() 的普通方程与曲线
的普通方程与曲线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)设曲线![]() 经过伸缩变换
经过伸缩变换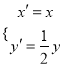 得到曲线
得到曲线![]() ,若点
,若点![]() ,直线
,直线![]() 与
与![]() 交与
交与![]() ,
, ![]() ,求
,求![]() ,
, ![]() .
.
参考答案:
【答案】(1)![]() 的普通方程为
的普通方程为![]() ,
, ![]() :
: ![]()
(2)![]() ;
; ![]()
【解析】试题分析:(1)直接消去参数t得直线l的普通方程,根据ρ2=x2+y2可得曲线C的直角坐标方程;(2)先根据伸缩变换得到曲线C′的方程,则![]() ,即可用韦达定理可得
,即可用韦达定理可得![]() ,
, ![]() 的值
的值
根据三角函数的性质可求出所求.
试题解析:(1)![]() 的普通方程为
的普通方程为![]() ,
, ![]() :
: ![]() ;
;
(2)根据条件可求出伸缩变换后的方程为![]() ,即
,即![]() ,直线
,直线![]() 的参数方程
的参数方程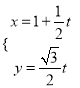 (
(![]() 为参数),带入椭圆:
为参数),带入椭圆: 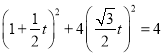 化简得
化简得![]() ,
, ![]() ,
, ![]() ,所以
,所以![]() ,
,
![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】经销商经销某种农产品,在一个销售季度内,每售出
 该产品获利润500元,未售出的产品,每
该产品获利润500元,未售出的产品,每 亏损300元.根据历史资料,得到销售季度内市场需求量的频率分布直图,如图所示.经销商为下一个销售季度购进了
亏损300元.根据历史资料,得到销售季度内市场需求量的频率分布直图,如图所示.经销商为下一个销售季度购进了 该农产品.以
该农产品.以 (
( )表示下一个销售季度内的市场需求量,
)表示下一个销售季度内的市场需求量,  (单位:元)表示下一个销售季度内经销该农产品的利润.
(单位:元)表示下一个销售季度内经销该农产品的利润.(Ⅰ)将
 表示为
表示为 的函数;
的函数;(Ⅱ)根据直方图估计利润
 不少于57000元的概率.
不少于57000元的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 .
.(1)用定义证明函数
 在
在 上是增函数;
上是增函数;(2)探究是否存在实数
 ,使得函数
,使得函数 为奇函数?若存在,求出
为奇函数?若存在,求出 的值;若不存在,请说明理由;
的值;若不存在,请说明理由;(3)在(2)的条件下,解不等式
 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线
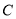 :
: 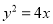 ,定点
,定点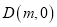 (常数
(常数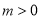 )的直线
)的直线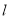 与曲线
与曲线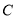 相交于
相交于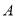 、
、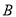 两点.
两点.(1)若点
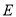 的坐标为
的坐标为 ,求证:
,求证: 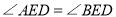
(2)若
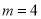 ,以
,以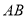 为直径的圆的位置是否恒过一定点?若存在,求出这个定点,若不存在,请说明理由.
为直径的圆的位置是否恒过一定点?若存在,求出这个定点,若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】某种新产品投放市场的100天中,前40天价格呈直线上升,而后60天其价格呈直线下降,现统计出其中4天的价格如下表:
时间
第4天
第32天
第60天
第90天
价格(千元)
23
30
22
7
(1)写出价格
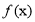 关于时间
关于时间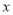 的函数关系式;(
的函数关系式;(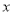 表示投放市场的第
表示投放市场的第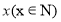 天);
天);(2)销售量
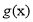 与时间
与时间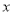 的函数关系:
的函数关系: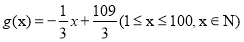 ,则该产品投放市场第几天销售额最高?最高为多少千元?
,则该产品投放市场第几天销售额最高?最高为多少千元? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形
 为梯形,
为梯形, 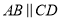 ,
, 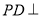 平面
平面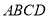 ,
, 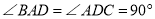 ,
, 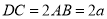 ,
, 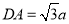 ,
, 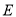 为
为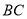 中点.
中点.(1)求证:平面
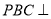 平面
平面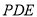 ;
;(2)线段
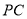 上是否存在一点
上是否存在一点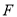 ,使
,使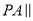 平面
平面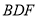 ?若有,请找出具体位置,并进行证明:若无,请分析说明理由.
?若有,请找出具体位置,并进行证明:若无,请分析说明理由.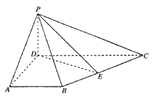
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
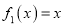 ,
, 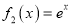 ,
, 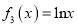 .
.(1)设函数
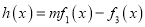 ,若
,若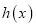 在区间
在区间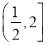 上单调,求实数
上单调,求实数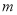 的取值范围;
的取值范围;(2)求证:
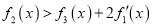 .
.
相关试题

