【题目】已知函数![]() (
(![]() ).
).
(Ⅰ)若曲线![]() 上点
上点![]() 处的切线过点
处的切线过点![]() ,求函数
,求函数![]() 的单调减区间;
的单调减区间;
(Ⅱ)若函数![]() 在
在![]() 上无零点,求
上无零点,求![]() 的最小值.
的最小值.
参考答案:
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ)![]() .
.
【解析】试题分析:(Ⅰ)由导数几何意义得切线斜率,再由点斜式得切线方程,代入点![]() 可解得
可解得![]() ,再根据函数
,再根据函数![]() 导函数小于零,解得单调减区间;(Ⅱ)先由题意得
导函数小于零,解得单调减区间;(Ⅱ)先由题意得![]() ,
,![]() 恒成立,再变量分离转化为对应函数最值:
恒成立,再变量分离转化为对应函数最值:![]() 的最大值,最后利用导数求函数
的最大值,最后利用导数求函数![]() ,
,![]() 最大值,经过二次求导可得
最大值,经过二次求导可得![]() 在区间
在区间![]() 内为增函数,
内为增函数,![]() ,因此
,因此![]() .
.
试题解析:(Ⅰ)因为![]() ,所以
,所以![]() ,
,
所以![]() ,又
,又![]() ,所以
,所以![]() ,得
,得![]() ,
,
由![]() ,得
,得![]() ,所以函数
,所以函数![]() 的单调减区间为
的单调减区间为![]() .
.
(Ⅱ)因为当![]() →
→![]() 时,
时,![]() ,所以
,所以![]() 在区间
在区间![]() 内恒成立不可能. 所以要使函数
内恒成立不可能. 所以要使函数![]() 在区间
在区间![]() 内无零点,只要对任意的
内无零点,只要对任意的![]() ,
,![]() 恒成立,即对
恒成立,即对![]() ,
,![]() 恒成立.
恒成立.
令![]() ,
,![]() ,则
,则![]() .
.
再令![]() ,
,![]() ,则
,则![]()
![]()
![]() ,
,
所以![]() 在区间
在区间![]() 内为减函数,所以
内为减函数,所以![]() ,
,
∴![]() .
.
于是![]() 在区间
在区间![]() 内为增函数,所以
内为增函数,所以![]() ,
,
所以要使![]() 恒成立,只要
恒成立,只要![]() .
.
综上,若函数![]() 在区间
在区间![]() 内无零点,则实数
内无零点,则实数![]() 的最小值为
的最小值为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
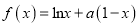 ,
, 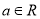 .
.(I)求
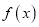 的单调区间;
的单调区间;(II)若对任意的
 ,都有
,都有 ,求实数
,求实数 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】制定投资计划时,不仅要考虑可能获得的盈利,而且要考虑可能出现的亏损.某投资人打算投资甲、乙两个项目.根据预测,甲、乙项目可能的最大盈利率分别为100%和50%,可能的最大亏损分别为30%和10%.投资人计划投资金额不超过10万元,要求确保可能的资金亏损不超过1.8万元.问投资人对甲、乙两个项目各投资多少万元,才能使可能的盈利最大?
-
科目: 来源: 题型:
查看答案和解析>>【题目】(本小题满分12分,第(1)问 4 分,第(2)问 8 分)
某闯关游戏规则是:先后掷两枚骰子,将此实验重复
 轮,第
轮,第 轮的点数分别记为
轮的点数分别记为 ,如果点数满足
,如果点数满足 ,则认为第
,则认为第 轮闯关成功,否则进行下一轮投掷,直到闯关成功,游戏结束。
轮闯关成功,否则进行下一轮投掷,直到闯关成功,游戏结束。求第一轮闯关成功的概率;
如果游戏只进行到第四轮,第四轮后不论游戏成功与否,都终止游戏,记进行的轮数为随机变量
 ,求
,求 的分布列和数学期望。
的分布列和数学期望。 -
科目: 来源: 题型:
查看答案和解析>>【题目】(本小题满分10分,第(1)问 5分,第(2)问 5 分)
近年来,微信越来越受欢迎,许多人通过微信表达自己、交流思想和传递信息,微信是现代生活中进行信息交流的重要工具.而微信支付为用户带来了全新的支付体验,支付环节由此变得简便而快捷.某商场随机对商场购物的
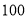 名顾客进行统计,其中
名顾客进行统计,其中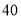 岁以下占
岁以下占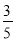 ,采用微信支付的占
,采用微信支付的占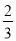 ,
, 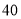 岁以上采用微信支付的占
岁以上采用微信支付的占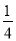 。
。(1)请完成下面
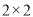 列联表:
列联表: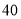 岁以下
岁以下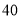 岁以上
岁以上合计
使用微信支付
未使用微信支付
合计
(2)并由列联表中所得数据判断有多大的把握认为“使用微信支付与年龄有关”?
参考公式:
 ,
, 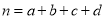 .
.参考数据:
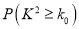

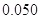
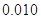

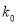
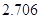
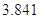
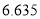
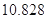
-
科目: 来源: 题型:
查看答案和解析>>【题目】【2017届安徽百校论坛高三文上学期联考二】已知函数
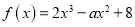 .
.(1)若
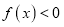 对
对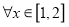 恒成立,求实数
恒成立,求实数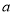 的取值范围;
的取值范围;(2)是否存在整数
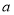 ,使得函数
,使得函数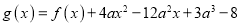 在区间
在区间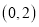 上存在极小值,若存在,求出所有整数
上存在极小值,若存在,求出所有整数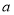 的值;若不存在,请说明理由.
的值;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】【2017届广东省珠海市高三上学期期末考试文数】已知函数
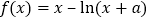 的最小值为0,其中
的最小值为0,其中 ,设
,设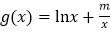 .
.(1)求
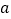 的值;
的值;(2)对任意
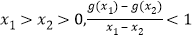 恒成立,求实数
恒成立,求实数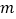 的取值范围;
的取值范围;(3)讨论方程
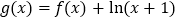 在
在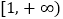 上根的个数.
上根的个数.
相关试题

