【题目】已知函数![]() ,
, ![]() .
.
(I)求![]() 的单调区间;
的单调区间;
(II)若对任意的![]() ,都有
,都有![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
参考答案:
【答案】(1)详见解析;(2) ![]() .
.
【解析】试题分析:对函数求导,针对参数![]() 进行讨论,研究函数得单调性;第二步为恒成立问题,当
进行讨论,研究函数得单调性;第二步为恒成立问题,当![]() 时,由于
时,由于![]() 不满足题意要求,当
不满足题意要求,当![]() 时,求出函数
时,求出函数![]() 的最大值,要使
的最大值,要使![]() 在
在![]() 上恒成立,只需
上恒成立,只需![]() ,从而求出
,从而求出![]() 的范围.
的范围.
试题解析:(I)![]() , 当
, 当![]() 时,
时, ![]() 恒成立,则
恒成立,则![]() 在
在![]() 上单调递增;当
上单调递增;当![]() 时,令
时,令![]() ,则
,则![]() .则
.则![]() 在区间
在区间![]() 上单调递增,在区间
上单调递增,在区间![]() 上单调递减.
上单调递减.
(II)方法1:
当![]() 时,因为
时,因为![]() ,
,
所以不会有![]() ,
, ![]() .
.
②当![]() 时,由(I)知,
时,由(I)知, ![]() 在
在![]() 上的最大值为
上的最大值为![]() .
.
所以![]() ,
, ![]() 等价于
等价于![]() .即
.即![]() .
.
设![]() ,由(I)知
,由(I)知![]() 在
在![]() 上单调递增.
上单调递增.
又![]() ,所以
,所以![]() 的解为
的解为![]() .
.
故![]() ,
, ![]() 时,实数
时,实数![]() 的取值范围是
的取值范围是![]() .
.
方法2: ![]() ,
, ![]() 等价于
等价于![]() .令
.令![]() ,则
,则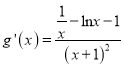 .
.
令![]() ,则
,则![]() .
.
因为当![]() ,
, ![]() 恒成立,
恒成立,
所以![]() 在
在![]() 上单调递减.
上单调递减.
又![]() ,可得
,可得![]() 和
和![]() 在
在![]() 上的情况如下:
上的情况如下:
|
|
|
|
| + | 0 | - |
| 单调递增 | 单调递减 |
所以![]() 在
在![]() 上的最大值为
上的最大值为![]() .
.
因此![]() ,
, ![]() 等价于
等价于![]() .
.
故![]() ,
, ![]() 时,实数
时,实数![]() 的取值范围是
的取值范围是![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某农科所对冬季昼夜温差大小与某反季节大豆新品种发芽多少之间的关系进行分析研究,他们分别记录了12月1日至12月5日的每天昼夜温差与实验室每天每100颗种子中的发芽数,得到如下资料:
日 期
12月1日
12月2日
12月3日
12月4日
12月5日
温差
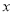 (°C)
(°C)10
11
13
12
8
发芽数
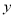 (颗)
(颗)23
25
30
26
16
该农科所确定的研究方案是:先从这五组数据中选取2组,用剩下的3组数据求线性回归方程,再对被选取的2组数据进行检验.
(1)求选取的2组数据恰好是不相邻2天数据的概率;
(2)若选取的是12月1日与12月5日的两组数据,请根据12月2日至12月4日的数据,求出y关于x的线性回归方程
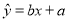 ;
;(3)若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2颗,则认为得到的线性回归方程是可靠的,试问(2)中所得的线性回归方程是否可靠?
(注:
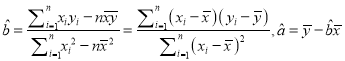 )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】【2017届湖北省武汉市武昌区高三1月调研考试文数】已知函数
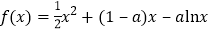 .
.(Ⅰ)讨论
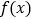 的单调性;
的单调性;(Ⅱ)设
 ,若对
,若对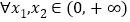 ,
, ,求
,求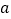 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知自变量x,y满足
 则当3≤S≤5时,z=3x+2y的最大值的变化范围为________.
则当3≤S≤5时,z=3x+2y的最大值的变化范围为________. -
科目: 来源: 题型:
查看答案和解析>>【题目】制定投资计划时,不仅要考虑可能获得的盈利,而且要考虑可能出现的亏损.某投资人打算投资甲、乙两个项目.根据预测,甲、乙项目可能的最大盈利率分别为100%和50%,可能的最大亏损分别为30%和10%.投资人计划投资金额不超过10万元,要求确保可能的资金亏损不超过1.8万元.问投资人对甲、乙两个项目各投资多少万元,才能使可能的盈利最大?
-
科目: 来源: 题型:
查看答案和解析>>【题目】(本小题满分12分,第(1)问 4 分,第(2)问 8 分)
某闯关游戏规则是:先后掷两枚骰子,将此实验重复
 轮,第
轮,第 轮的点数分别记为
轮的点数分别记为 ,如果点数满足
,如果点数满足 ,则认为第
,则认为第 轮闯关成功,否则进行下一轮投掷,直到闯关成功,游戏结束。
轮闯关成功,否则进行下一轮投掷,直到闯关成功,游戏结束。求第一轮闯关成功的概率;
如果游戏只进行到第四轮,第四轮后不论游戏成功与否,都终止游戏,记进行的轮数为随机变量
 ,求
,求 的分布列和数学期望。
的分布列和数学期望。 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
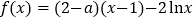 (
(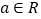 ).
).(Ⅰ)若曲线
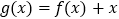 上点
上点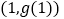 处的切线过点
处的切线过点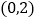 ,求函数
,求函数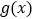 的单调减区间;
的单调减区间;(Ⅱ)若函数
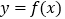 在
在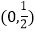 上无零点,求
上无零点,求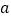 的最小值.
的最小值.
相关试题

