【题目】国内某知名连锁店分店开张营业期间,在固定的时间段内消费达到一定标准的顾客可进行一次抽奖活动,随着抽奖活动的有效开展,参与抽奖活动的人数越来越多,该分店经理对开业前![]() 天参加抽奖活动的人数进行统计,
天参加抽奖活动的人数进行统计, ![]() 表示开业第
表示开业第![]() 天参加抽奖活动的人数,得到统计表格如下:
天参加抽奖活动的人数,得到统计表格如下:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
经过进一步统计分析,发现![]() 与
与![]() 具有线性相关关系.
具有线性相关关系.
(1)根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)若该分店此次抽奖活动自开业始,持续![]() 天,参加抽奖的每位顾客抽到一等奖(价值
天,参加抽奖的每位顾客抽到一等奖(价值![]() 元奖品)的概率为
元奖品)的概率为![]() ,抽到二等奖(价值
,抽到二等奖(价值![]() 元奖品)的概率为
元奖品)的概率为![]() ,抽到三等奖(价值
,抽到三等奖(价值![]() 元奖品)的概率为
元奖品)的概率为![]() .
.
试估计该分店在此次抽奖活动结束时送出多少元奖品?
参考公式: 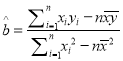 ,
, ![]() .
.
参考答案:
【答案】(1)![]() (2)
(2)![]()
【解析】试题分析:(1)由公式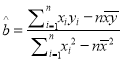 ,可得
,可得![]() ,再求均值
,再求均值![]() ,并由
,并由![]() 可得
可得![]() ,进而可得线性回归方程
,进而可得线性回归方程![]() ;(2)先根据数学期望公式求每位获奖奖金的期望
;(2)先根据数学期望公式求每位获奖奖金的期望![]() ,再根据线性回归方程预测第8,9,10天人数,得到10天总人数,最后根据乘积得到总奖金数.
,再根据线性回归方程预测第8,9,10天人数,得到10天总人数,最后根据乘积得到总奖金数.
试题解析:(1)依题意: ![]() ,
,
![]() ,
,
![]() ,
,
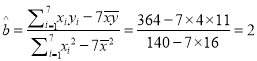 ,
, ![]() ,
,
则![]() 关于
关于![]() 的线性回归方程为
的线性回归方程为![]() .
.
(2)参加抽奖的每位顾客获得奖品金额为![]() ,
, ![]() 的分布列为
的分布列为
|
|
|
|
|
|
|
|
![]() (元).
(元).
由![]() 关于
关于![]() 的回归直线方程
的回归直线方程![]() ,预测
,预测![]() 时
时![]() ,
, ![]() 时
时![]() ,
, ![]() 时
时![]() ,
,
则此次活动参加抽奖的人数约为![]() 人,
人,
![]() (元),
(元),
所以估计该分店在此次抽奖活动结束时送出![]() 元奖品.
元奖品.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市为了宣传环保知识,举办了一次“环保知识知多少”的问卷调查活动(一人答一份).现从回收的年龄在2060岁的问卷中随机抽取了100份, 统计结果如下面的图表所示.
年龄
分组
抽取份
数
答对全卷的人数
答对全卷的人数占本组的概率
[20,30)
40
28
0.7
[30,40)
n
27
0.9
[40,50)
10
4
b
[50,60]
20
a
0.1
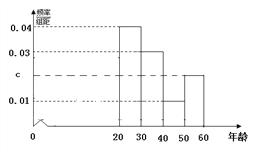
(1)分别求出n, a, b, c的值;
(2)从年龄在[40,60]答对全卷的人中随机抽取2人授予“环保之星”,求年龄在[50,60] 的人中至少有1人被授予“环保之星”的概率.
-
科目: 来源: 题型:
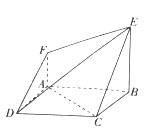
查看答案和解析>>【题目】如图所示的空间几何体中,底面四边形
 为正方形,
为正方形, 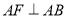 ,
,  ,平面
,平面 平面
平面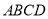 ,
, 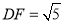 ,
, 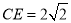 ,
, 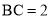 .
.
(1)求二面角
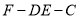 的大小;
的大小;(2)若在平面
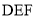 上存在点
上存在点 ,使得
,使得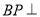 平面
平面 ,试通过计算说明点
,试通过计算说明点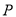 的位置.
的位置. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,已知AB丄平面BCD,M、N分别是AC、AD的中点,BC 丄 CD.

(1)求证:MN//平面BCD;
(2)若AB=1,BC=
 ,求直线AC与平面BCD所成的角.
,求直线AC与平面BCD所成的角. -
科目: 来源: 题型:
查看答案和解析>>【题目】【2016-2017学年辽宁省六校协作体高二下学期期初数学(理)】已知圆
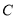 的圆心在坐标原点,且与直线
的圆心在坐标原点,且与直线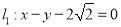 相切.
相切.(1)求直线
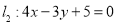 被圆
被圆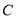 所截得的弦
所截得的弦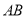 的长;
的长;(2)过点
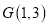 作两条与圆
作两条与圆 相切的直线,切点分别为
相切的直线,切点分别为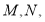 求直线
求直线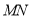 的方程;
的方程;(3)若与直线
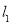 垂直的直线
垂直的直线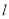 与圆
与圆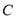 交于不同的两点
交于不同的两点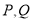 ,若
,若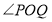 为钝角,求直线
为钝角,求直线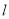 在
在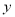 轴上的截距的取值范围.
轴上的截距的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,三棱柱A1B1C1 - ABC中,侧棱AA1丄底面A1B1C1,底面三角形A1B1C1是正三角形,E是BC中点,则下列叙述正确的是

A. CC1与B1E是异面直线 B. AC丄平面ABB1A1
C. A1C1∥平面AB1E D. AE与B1C1为异面直线,且AE丄B1C1
-
科目: 来源: 题型:
查看答案和解析>>【题目】【河南省2017届高中毕业年级考前预测数学(理)】已知圆
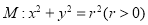 与直线
与直线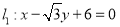 相切,设点
相切,设点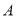 为圆上一动点,
为圆上一动点, 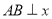 轴于
轴于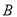 ,且动点
,且动点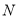 满足
满足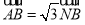 ,设动点
,设动点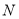 的轨迹为曲线
的轨迹为曲线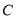 .
.(1)求曲线
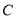 的方程;
的方程;(2)直线
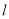 与直线
与直线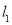 垂直且与曲线
垂直且与曲线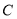 交于
交于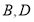 两点,求
两点,求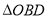 面积的最大值.
面积的最大值.
相关试题

