【题目】如图,在棱长为![]() 的正方体
的正方体![]() 中,
中,![]() ,
,![]() 分别在棱
分别在棱![]() ,
,![]() 上,且
上,且![]() .
.
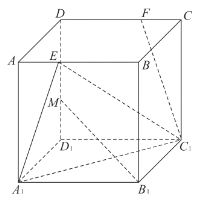
(1)已知![]() 为棱
为棱![]() 上一点,且
上一点,且![]() ,求证:
,求证:![]() 平面
平面![]() .
.
(2)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
参考答案:
【答案】(1)见解析;(2)![]()
【解析】
(1)过M作MT⊥AA1于点T,连B1T,则A1T=1.推导出△AA1E≌△A1B1T,∠AA1E=∠A1B1T.推导出A1E⊥B1T.从而MT⊥面AA1B1B,进而MT⊥A1E,A1E⊥面MTB,A1E⊥MB1.连B1D1,则B1D1⊥A1C1.又D1M⊥A1C1,从而A1C1⊥面MD1B1,A1C1⊥MB1.由A1E⊥MB1,A1C1⊥MB1,能证明B1M⊥面A1EC1.
(2)在D1C1上取一点N,使ND1=1,连接EF.则![]() .
.![]() =
=![]() .由余弦定理可知cos∠EA1C1.求出△A1EC1的面积,由等体积法可知F到平面A1EC1之距离h满足
.由余弦定理可知cos∠EA1C1.求出△A1EC1的面积,由等体积法可知F到平面A1EC1之距离h满足![]() ,求出
,求出![]() ,由此能求出直线FC1与平面A1EC1所成角的正弦值.
,由此能求出直线FC1与平面A1EC1所成角的正弦值.
(1)过![]() 作
作![]() 于点
于点![]() ,连
,连![]() ,则
,则![]() .易证:
.易证:![]() ,于是
,于是![]() .由
.由![]() ,知
,知![]() ,∴
,∴![]() .显然
.显然![]() 面
面![]() ,而
,而![]() 面
面![]() ,∴
,∴![]() ,又
,又![]() ,∴
,∴![]() 面
面![]() ,∴
,∴![]() .连
.连![]() ,则
,则![]() .
.
又![]() ,
,![]() ,∴
,∴![]() 面
面![]() ,∴
,∴![]() .由
.由![]() ,
,![]() ,
,![]() ,∴
,∴![]() 面
面![]() .
.
(2)在![]() 上取一点
上取一点![]() ,使
,使![]() ,连接
,连接![]() .易知
.易知![]() .∴
.∴![]()
![]() .对于
.对于![]() ,
,![]() ,
,![]() ,而
,而![]() ,
,
由余弦定理可知![]() .∴
.∴![]() 的面积
的面积![]()
![]() .由等体积法可知
.由等体积法可知![]() 到平面
到平面![]() 之距离
之距离![]() 满足
满足![]() ,则
,则![]() ,∴
,∴![]() ,又
,又![]() ,设
,设![]() 与平面
与平面![]() 所成角为
所成角为![]() ,∴
,∴![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】按照《国务院关于印发“十三五”节能减排综合工作方案的通知》(国发[2016〕74号)的要求,到2020年,全国化学需氧量排放总量要控制在2001万吨以内,要比2015年下降10%假设“十三五”期间每一年化学需氧量排放总量下降的百分比都相等,2015年后第
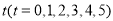 年的化学需氧量排放总量最大值为
年的化学需氧量排放总量最大值为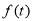 万吨.
万吨.(1)求
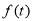 的解析式;
的解析式;(2)求2019年全国化学需氧量排放总量要控制在多少万吨以内(精确到1万吨).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 单调递增,函数
单调递增,函数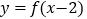 的图像关于点
的图像关于点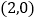 对称,实数
对称,实数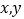 满足不等式
满足不等式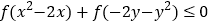 ,则
,则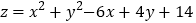 的最小值为( )
的最小值为( )A.
 B.
B.  C.
C. 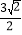 D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】《九章算术》第八章“方程”问题八:今有卖牛二、羊五,以买十三豕,有余钱一千。卖牛三、豕三,以买九羊,钱适足.卖羊六、豕八,以买五牛,钱不足六百.问牛、羊、豕各几何?“如果卖掉2头牛和5只羊,可买13口猪,还余1000钱;卖掉3头牛和3口猪的钱恰好可买9只羊;而卖掉6只羊和8口猪,去买5头牛,还少600钱.问牛、羊、猪的价格各是多少”.按照题意,可解出牛______钱、羊______钱、猪______钱.
-
科目: 来源: 题型:
查看答案和解析>>【题目】近年来,太阳能技术运用的步伐日益加快.2002年全球太阳能电池的年生产量达到670 MW,年生产量的增长率为34%.以后四年中,年生产量的增长率逐年递增2%(如,2003年的年生产量的增长率为36%).
(1)求2006年全球太阳能电池的年生产量(结果精确到0.1 MW);
(2)目前太阳能电池产业存在的主要问题是市场安装量远小于生产量,2006年的实际安装量为1420MW.假设以后若干年内太阳能电池的年生产量的增长率保持在42%,到2010年,要使年安装量与年生产量基本持平(即年安装量不少于年生产量的95%),这四年中太阳能电池的年安装量的平均增长率至少应达到多少(结果精确到0.1%)?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在正方体
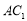 中,
中,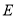 、
、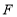 分别为
分别为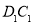 、
、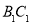 的中点,
的中点,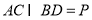 ,
,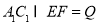 ,如图.
,如图.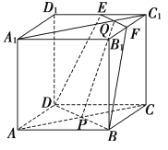
(1)若
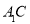 交平面
交平面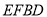 于点
于点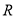 ,证明:
,证明: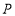 、
、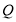 、
、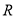 三点共线;
三点共线;(2)线段
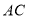 上是否存在点
上是否存在点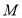 ,使得平面
,使得平面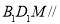 平面
平面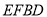 ,若存在确定
,若存在确定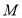 的位置,若不存在说明理由.
的位置,若不存在说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直四棱柱
 的底面是直角梯形,
的底面是直角梯形,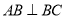 ,
,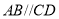 ,
,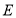 、
、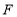 分别是棱
分别是棱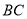 、
、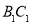 上的动点,且
上的动点,且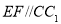 ,
,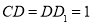 ,
,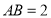 ,
,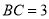 .
.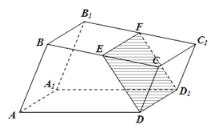
(1)证明:无论点
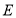 怎样运动,四边形
怎样运动,四边形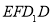 都为矩形;
都为矩形;(2)当
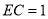 时,求几何体
时,求几何体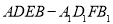 的体积.
的体积.
相关试题

