【题目】在棱长为![]() 的正方体上,分别用过共顶点的三条棱中点的平面截该正方形,则截去
的正方体上,分别用过共顶点的三条棱中点的平面截该正方形,则截去![]() 个三棱锥后,剩下的几何体的体积是( ).
个三棱锥后,剩下的几何体的体积是( ).
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
参考答案:
【答案】C
【解析】每个三棱锥的体积![]() ,
,
剩下几何体的体积![]() ,
,
故选![]() .
.
点睛:求体积的一些特殊方法——分割法、补形法、等体积法. ①割补法:求一些不规则几何体的体积时,常用割补法转化成已知体积公式的几何体进行解决.②等积法:等积法包括等面积法和等体积法.等积法的前提是几何图形(或几何体)的面积(或体积)通过已知条件可以得到,利用等积法可以用来求解几何图形的高或几何体的高,特别是在求三角形的高和三棱锥的高时,这一方法回避了通过具体作图得到三角形(或三棱锥)的高,而通过直接计算得到高的数值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】己知圆
 的圆心在直线
的圆心在直线 上,且过点
上,且过点 ,与直线
,与直线 相切.
相切.(
 )求圆
)求圆 的方程.
的方程.(
 )设直线
)设直线 与圆
与圆 相交于
相交于 ,
, 两点.求实数
两点.求实数 的取值范围.
的取值范围.(
 )在(
)在( )的条件下,是否存在实数
)的条件下,是否存在实数 ,使得弦
,使得弦 的垂直平分线
的垂直平分线 过点
过点 ,若存在,求出实数
,若存在,求出实数 的值;若不存在,请说明理由.
的值;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,三棱锥
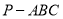 的三个侧面均为边长是
的三个侧面均为边长是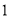 的等边三角形,
的等边三角形, 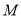 ,
, 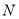 分别为
分别为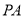 ,
, 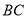 的中点.
的中点.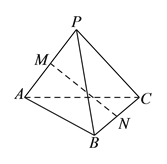
(I)求
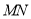 的长.
的长.(II)求证:
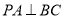 .
.(III)求三棱锥
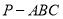 的表面积.
的表面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知四棱锥P﹣ABCD,底面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,E、F分别是BC、PC的中点.
(1)判定AE与PD是否垂直,并说明理由.
(2)设AB=2,若H为PD上的动点,若△AHE面积的最小值为 , 求四棱锥P﹣ABCD的体积.
, 求四棱锥P﹣ABCD的体积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
在平面直角坐标系中,直线
 的参数方程为
的参数方程为 ,其中
,其中 为参数,
为参数,  ,再以坐标原点
,再以坐标原点 为极点,以
为极点,以 轴正半轴为极轴,建立极坐标系,曲线
轴正半轴为极轴,建立极坐标系,曲线 的极坐标方程为
的极坐标方程为 ,其中
,其中 ,
, 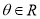 ,直线
,直线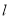 与曲线
与曲线 交于
交于 两点.
两点.(1)求
 的值;
的值;(2)已知点
 ,且
,且 ,求直线
,求直线 的普通方程.
的普通方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】把不等式组
 的解集表示在数轴上,正确的是( )
的解集表示在数轴上,正确的是( )
A.
B.
C.
D.
-
科目: 来源: 题型:
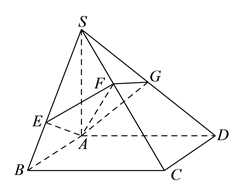
查看答案和解析>>【题目】如图,已知矩形
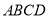 ,过
,过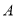 作
作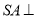 平面
平面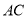 ,再过
,再过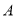 作
作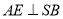 于点
于点 ,过
,过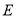 作
作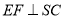 于点
于点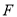 .
.(Ⅰ)求证:
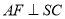 .
.(Ⅱ)若平面
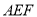 交
交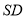 于点
于点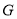 ,求证:
,求证: 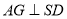 .
.
相关试题

