【题目】政府鼓励创新、创业,银行给予低息贷款.一位大学毕业生向自主创业,经过市场调研、测算,有两个方案可供选择.
方案1:开设一个科技小微企业,需要一次性贷款40万元,第一年获利是贷款额的10%,以后每年比上一年增加25%的利润.
方案2:开设一家食品小店,需要一次性贷款20万元,第一年获利是贷款额的15%,以后每年比上一年增加利润1.5万元.两种方案使用期限都是10年,到期一次性还本付息.两种方案均按年息2%的复利计算(参考数据:1.259=7.45,1.2510=9.3,1.029=1.20,1.0210=1.22).
(1)10年后,方案1,方案2的总收入分别有多少万元?
(2)10年后,哪一种方案的利润较大?
参考答案:
【答案】
(1)解:方案1是等比数列,方案2是等差数列,
①方案1,一次性贷款40万元,第一年获利是贷款额的10%,即4万元
获利:4[1+(1+25%)+(1+25%)2+…+(1+25%)9]=4× ![]() =132.8(万元),
=132.8(万元),
银行贷款本息:40(1+2%)10≈48.8(万元),
方案2,一次性贷款20万元,第一年获利是贷款额的15%,即3万元
获利:3+(3+1.5)+(3+2×1.5)+…+(3+9×1.5)
=10×3+ ![]() =97.50(万元)
=97.50(万元)
(2)解:方案1,银行贷款本息:40(1+2%)10≈12.2(万元),
故方案1纯利:132.8﹣48.8=84(万元).
方案2,银行贷款本息:20(1+2%)10≈24.4(万元),
故方案2纯利:97.50﹣24.4=73.1(万元).
∴方案1的利润较大.
【解析】(1)方案1是等比数列,方案2是等差数列,利用求和公式,可得结论;(2)计算银行贷款本息,可得纯利,即可得出哪一种方案的利润较大.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=
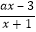 (a∈R).
(a∈R).
(1)若不等式f(x)<1的解集为(﹣1,4),求a的值;
(2)设a≤0,解关于x的不等式f(x)>0. -
科目: 来源: 题型:
查看答案和解析>>【题目】一个几何体的三视图及尺寸如图所示,则该几何体的外接球半径为( )

A.
B.
C.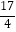
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设△ABC的内角A,B,C的对边分别为a,b,c,已知4sinA=4cosBsinC+bsin2C,且C≠
 .
.
(1)求c;
(2)若C=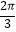 ,求△ABC周长的取值范围.
,求△ABC周长的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=x﹣
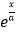 存在单调递减区间,且y=f(x)的图象在x=0处的切线l与曲线y=ex相切,符合情况的切线l( )
存在单调递减区间,且y=f(x)的图象在x=0处的切线l与曲线y=ex相切,符合情况的切线l( )
A.有3条
B.有2条
C.有1条
D.不存在 -
科目: 来源: 题型:
查看答案和解析>>【题目】设函数f(x)=a2x+
 (a,b,c为常数,且a>0,c>0).
(a,b,c为常数,且a>0,c>0).
(1)当a=1,b=0时,求证:|f(x)|≥2c;
(2)当b=1时,如果对任意的x>1都有f(x)>a恒成立,求证:a+2c>1. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列{an}的前n项和Sn=2n2+n,n∈N* .
(1)求{an}的通项公式;
(2)若数列{bn}满足an=4log2bn+3,n∈N* , 求数列{anbn}的前n项和Tn .
相关试题

