

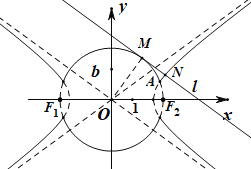
【题目】已知双曲线![]() 与圆
与圆![]() 在第一象限交点为
在第一象限交点为![]() ,曲线
,曲线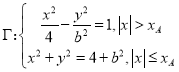 .
.
(1)若![]() ,求b;
,求b;
(2)若![]() ,
,![]() 与x轴交点是
与x轴交点是![]() ,P
,P![]() 是曲线
是曲线![]() 上一点,且在第一象限,并满足
上一点,且在第一象限,并满足![]() ,求∠
,求∠![]() ;
;
(3)过点![]() 且斜率为
且斜率为![]() 的直线
的直线![]() 交曲线
交曲线![]() 于M、N两点,用b的代数式表示
于M、N两点,用b的代数式表示![]() ,并求出
,并求出![]() 的取值范围.
的取值范围.
【答案】(1)2;(2)![]() ;(3)
;(3)![]() ;
;![]() .
.
【解析】
(1)根据双曲线和圆的方程,将点![]() 的坐标代入,得到方程组,求得
的坐标代入,得到方程组,求得![]() 的值;
的值;
(2)方法一:结合双曲线的定义,得到![]() 的三边长,利用余弦定理求解;
的三边长,利用余弦定理求解;
方法二:根据![]() ,和双曲线的方程,联立方程组,求得
,和双曲线的方程,联立方程组,求得![]() 的坐标,进而利用向量的坐标运算和向量的夹角余弦值公式求解;
的坐标,进而利用向量的坐标运算和向量的夹角余弦值公式求解;
(3)根据直线![]() 的方程,判定是圆的切线,切点为
的方程,判定是圆的切线,切点为![]() ,并利用直线
,并利用直线![]() 的方程与圆的方程联立求得
的方程与圆的方程联立求得![]() 的坐标,注意到直线
的坐标,注意到直线![]() 与双曲线的斜率为负值的渐近线平行,利用数形结合思想,可得只有当
与双曲线的斜率为负值的渐近线平行,利用数形结合思想,可得只有当![]() 时,直线
时,直线![]() 才能与曲线
才能与曲线![]() 有两个交点,然后联立圆和双曲线的方程,求得
有两个交点,然后联立圆和双曲线的方程,求得![]() 的纵坐标关于
的纵坐标关于![]() 的函数表达式,进而解不等式求得
的函数表达式,进而解不等式求得![]() ,最后利用向量的数量积的运算得到
,最后利用向量的数量积的运算得到![]() 的取值范围.
的取值范围.
(1)若![]() ,因为点A为曲线
,因为点A为曲线![]() 与曲线
与曲线![]() 的交点,
的交点,
∵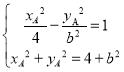 ,解得
,解得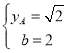 ,
,
∴![]() ;
;
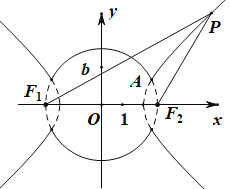
(2)方法一:由题意易得![]() 为曲线的两焦点,因为
为曲线的两焦点,因为![]() ∴
∴![]() ,
,
又∵P在第一象限,由双曲线定义知:![]() ,
,
![]() ,∴
,∴![]() ,
,
又∵![]() ,∴
,∴![]() ,
,
在![]() 中由余弦定理可得:
中由余弦定理可得:
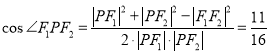 ;
;
方法二:∵![]() ,可得
,可得 ,解得
,解得![]() ,
,
![]()
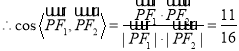 ;
;
(3)设直线![]() ,
,
可得原点O到直线![]() 的距离
的距离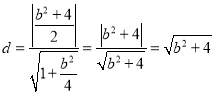 ,
,
所以直线![]() 是圆的切线,切点为M,
是圆的切线,切点为M,
所以![]() ,并设
,并设![]() ,与圆
,与圆![]() 联立可得
联立可得![]() ,
,
所以得![]() ,即
,即![]() ,
,
直线![]() 的斜率为
的斜率为![]() ,双曲线的渐近线方程为
,双曲线的渐近线方程为![]() ,
,
所以直线![]() 与双曲线的斜率为负值的渐近线平行,
与双曲线的斜率为负值的渐近线平行,
所以只有当![]() 时,直线
时,直线![]() 才能与曲线
才能与曲线![]() 有两个交点,
有两个交点,
由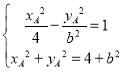 ,得
,得![]() ,
,
所以有![]() ,得
,得![]() ,
,
又因为:![]() ,
,
所以![]() .
.


 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案科目:高中数学 来源: 题型:
【题目】已知抛物线![]() :
:![]() (
(![]() ).
).
(1)若抛物线![]() 的焦点到准线的距离为4,点
的焦点到准线的距离为4,点![]() ,
,![]() 在抛物线
在抛物线![]() 上,线段
上,线段![]() 的中点为
的中点为![]() ,求直线
,求直线![]() 的方程;
的方程;
(2)若圆![]() 以原点
以原点![]() 为圆心,1为半径,直线
为圆心,1为半径,直线![]() 与
与![]() ,
,![]() 分别相切,切点分别为
分别相切,切点分别为![]() ,
,![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市政府为了节约生活用电,计划在本市试行居民生活用电定额管理,即确定一户居民月用电量标准a,用电量不超过a的部分按平价收费,超出a的部分按议价收费![]() 为此,政府调查了100户居民的月平均用电量
为此,政府调查了100户居民的月平均用电量![]() 单位:度
单位:度![]() ,以
,以![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分组的频率分布直方图如图所示.
分组的频率分布直方图如图所示.
![]() 根据频率分布直方图的数据,求直方图中x的值并估计该市每户居民月平均用电量
根据频率分布直方图的数据,求直方图中x的值并估计该市每户居民月平均用电量![]() 的值;
的值;
![]() 用频率估计概率,利用
用频率估计概率,利用![]() 的结果,假设该市每户居民月平均用电量X服从正态分布
的结果,假设该市每户居民月平均用电量X服从正态分布![]()
![]() 估计该市居民月平均用电量介于
估计该市居民月平均用电量介于![]() 度之间的概率;
度之间的概率;
![]() 利用
利用![]() 的结论,从该市所有居民中随机抽取3户,记月平均用电量介于
的结论,从该市所有居民中随机抽取3户,记月平均用电量介于![]() 度之间的户数为
度之间的户数为![]() ,求
,求![]() 的分布列及数学期望
的分布列及数学期望![]() .
.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有以下命题:
①存在实数![]() ,
,![]() ,使得
,使得![]() ;
;
②“![]() ,
,![]() ”的否定是“存在
”的否定是“存在![]() ,
,![]() ”;
”;
③掷一枚质地均匀的正方体骰子,向上的点数不小于3的概率为![]() ;
;
④在闭区间![]() 上取一个随机数
上取一个随机数![]() ,则
,则![]() 的概率为
的概率为![]() .
.
其中所有的真命题为________.(填写所有正确的结论序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》是我国古代的数学名著,书中有如下问题:“今有五人分五钱,令上两人所得与下三人等。问各得几何?”其意思是:“已知甲、乙、丙、丁、戊五人分五钱,甲、乙两人所得之和与丙、丁、戊三人所得之和相等,且甲、乙、丙、丁、戊所得依次成等差数列。问五人各得多少钱?”(“钱”是古代的一种重量单位)。这个问题中,戊所得为( )
A. ![]() 钱 B.
钱 B. ![]() 钱 C.
钱 C. ![]() 钱 D.
钱 D. ![]() 钱
钱
查看答案和解析>>
科目:高中数学 来源: 题型:
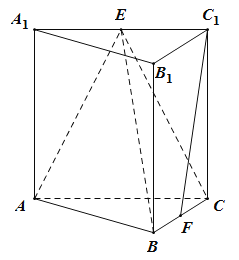
【题目】如图,在正三棱柱![]() 中底面边长、侧棱长都是4,
中底面边长、侧棱长都是4,![]() 别是
别是![]() 的中点,则以下四个结论中正确的是( )
的中点,则以下四个结论中正确的是( )
①![]() 与
与![]() 所成的角的余弦值为
所成的角的余弦值为![]() ;②
;②![]() 平行于平面
平行于平面![]() ;③三棱锥
;③三棱锥![]() 的体积为
的体积为![]() ;④
;④![]() 垂直于
垂直于![]() .
.
A.①②③B.②③④C.①③④D.①②④
查看答案和解析>>
科目:高中数学 来源: 题型:
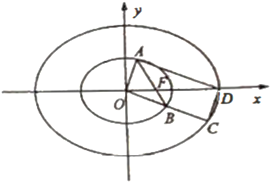
【题目】在平面直角坐标系![]() 中,已知椭圆
中,已知椭圆![]() 与
与![]() 的离心率相等.椭圆
的离心率相等.椭圆![]() 的右焦点为F,过点F的直线与椭圆
的右焦点为F,过点F的直线与椭圆![]() 交于A,B两点,射线
交于A,B两点,射线![]() 与椭圆
与椭圆![]() 交于点C,椭圆
交于点C,椭圆![]() 的右顶点为D.
的右顶点为D.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若![]() 的面积为
的面积为![]() ,求直线
,求直线![]() 的方程;
的方程;
(3)若![]() ,求证:四边形
,求证:四边形![]() 是平行四边形.
是平行四边形.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解甲、乙两种产品的质量,从中分别随机抽取了10件样品,测量产品中某种元素的含量(单位:毫克),如图所示是测量数据的茎叶图.规定:当产品中的此中元素的含量不小于18毫克时,该产品为优等品.
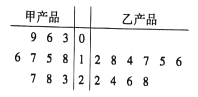
(1)试用样品数据估计甲、乙两种产品的优等品率;
(2)从乙产品抽取的10件样品中随机抽取3件,求抽到的3件样品中优等品数![]() 的分布列及其数学期望
的分布列及其数学期望![]() ;
;
(3)从甲产品抽取的10件样品中有放回地随机抽取3件,也从乙产品抽取的10件样品中有放回地随机抽取3件;抽到的优等品中,记“甲产品恰比乙产品多2件”为事件![]() ,求事件
,求事件![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,已知抛物线
中,已知抛物线![]() ,过点
,过点![]() 的直线
的直线![]() 交抛物线于
交抛物线于![]() ,
,![]() ,
,![]() ,
,![]() 两点.当
两点.当![]() 垂直于
垂直于![]() 轴时,
轴时,![]() 的面积为
的面积为![]() .
.
0
(1)求抛物线的方程:
(2)设线段![]() 的垂直平分线交
的垂直平分线交![]() 轴于点
轴于点![]() .
.
①证明:![]() 为定值:
为定值:
②若![]() ,求直线
,求直线![]() 的斜率.
的斜率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com