【题目】设![]() 是由
是由![]() 个实数组成的有序数组,满足下列条件:①
个实数组成的有序数组,满足下列条件:①![]() ,
,![]() ;②
;②![]() ;③
;③![]() ,
,
![]() .
.
(Ⅰ)当![]() 时,写出满足题设条件的全部
时,写出满足题设条件的全部![]() ;
;
(Ⅱ)设![]() ,其中
,其中![]() ,求
,求![]() 的取值集合;
的取值集合;
(Ⅲ)给定正整数![]() ,求
,求![]() 的个数.
的个数.
参考答案:
【答案】(1) 详见解析;(2) ![]() ; (3)
; (3) ![]()
【解析】试题分析:
(Ⅰ)利用题中所定义的![]() 可得
可得![]() 共有5个可能的值;
共有5个可能的值;
(Ⅱ)利用题意逐一交换元素的位置,讨论可得:![]() 的取值集合为
的取值集合为![]() .
.
(Ⅲ)利用(II)中的方法结合排列组合相关结论可得给定正整数![]() ,求
,求![]() 的个数是
的个数是![]()
试题解析:
(Ⅰ)解:![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,共
,共![]() 个.
个.
(Ⅱ)解:首先证明![]() ,且
,且![]() .
.
在③中,令![]() ,得
,得![]() .由①得
.由①得![]() .
.
由②得![]() .
.
在③中,令![]() ,得
,得![]() ,
,
从而![]() .由①得
.由①得![]() .
.
考虑![]() ,即
,即![]() ,
,![]() ,此时
,此时![]() 为最大值.
为最大值.
现交换![]() 与
与![]() ,使得
,使得![]() ,此时
,此时![]() .
.
现将![]() 逐项前移,直至
逐项前移,直至![]() .在前移过程中,显然
.在前移过程中,显然![]() 不变,这一过程称为1次移位.
不变,这一过程称为1次移位.
继续交换![]() 与
与![]() ,使得
,使得![]() ,此时
,此时![]() .
.
现将![]() 逐项前移,直至
逐项前移,直至![]() .在前移过程中,显然
.在前移过程中,显然![]() 不变,执行第2次移位.
不变,执行第2次移位.
依此类推,每次移位![]() 的值依次递减
的值依次递减![]() .经过有限次移位,
.经过有限次移位,![]() 一定可以调整为
一定可以调整为![]() ,
,![]() 交替出现.
交替出现.
注意到![]() 为奇数,所以
为奇数,所以![]() 为最小值.
为最小值.
所以,![]() 的取值集合为
的取值集合为![]() .
.
(Ⅲ)解:由①、②可知,有序数组![]() 中,有
中,有![]() 个
个![]() ,
,![]() 个
个![]() .
.
显然,从![]() 中选
中选![]() 个
个![]() ,其余为
,其余为![]() 的种数共有
的种数共有![]() 种.下面我们考虑这样的数组中有多少个不满足条件③,记该数为
种.下面我们考虑这样的数组中有多少个不满足条件③,记该数为![]() .
.
如果![]() 不满足条件③,则一定存在最小的正整数
不满足条件③,则一定存在最小的正整数![]() ,使得
,使得
(ⅰ)![]() ; (ⅱ)
; (ⅱ)![]() .
.
将![]() 统统改变符号,
统统改变符号,
这一对应![]() 为:
为:![]() ,
,
从而将![]() 变为
变为![]() 个
个![]() ,
,![]() 个
个![]() 组成的有序数组.
组成的有序数组.
反之,任何一个![]() 个
个![]() ,
,![]() 个
个![]() 组成的有序数组
组成的有序数组![]() .由于
.由于![]() 多于
多于![]() 的个数,所以一定存在最小的正整数
的个数,所以一定存在最小的正整数![]() ,使得
,使得![]() .
.
令对应![]() 为:
为:![]() ,
,
从而将![]() 变为
变为![]() 个
个![]() ,
,![]() 个
个![]() 组成的有序数组.
组成的有序数组.
因此,![]() 就是
就是![]() 个
个![]() ,
,![]() 个
个![]() 组成的有序数组的个数.
组成的有序数组的个数.
所以![]() 的个数是
的个数是![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)对定义域R内的任意x都有f(x)=f(4﹣x),且当x≠2时其导函数f′(x)满足(x﹣2)f′(x)>0,若2<a<4则( )
A.f(2a)<f(3)<f(log2a)
B.f(log2a)<f(3)<f(2a)
C.f(3)<f(log2a)<f(2a)
D.f(log2a)<f(2a)<f(3) -
科目: 来源: 题型:
查看答案和解析>>【题目】设a,b∈R,ab≠0,给出下面四个命题:①a2+b2≥﹣2ab;②
 ≥2;③若a<b,则ac2<bc2;④若
≥2;③若a<b,则ac2<bc2;④若  .则a>b;其中真命题有( )
.则a>b;其中真命题有( )
A.1
B.2
C.3
D.4 -
科目: 来源: 题型:
查看答案和解析>>【题目】过抛物线y2=2px(p>0)的焦点F的直线l与抛物线在第一象限的交点为A,与抛物线的准线的交点为B,点A在抛物线准线上的射影为C,若
 =
=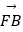 ,
,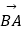

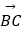 =48,则抛物线的方程为( )
=48,则抛物线的方程为( )
A.y2=4x
B.y2=8x
C.y2=16x
D.y2=4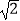 X
X -
科目: 来源: 题型:
查看答案和解析>>【题目】设P,Q是两个集合,定义集合P﹣Q={x|x∈P且xQ}为P,Q的“差集”,已知P={x|1﹣
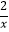 <0},Q={x||x﹣2|<1},那么P﹣Q等于( )
<0},Q={x||x﹣2|<1},那么P﹣Q等于( )
A.{x|0<x<1}
B.{x|0<x≤1}
C.{x|1≤x<2}
D.{x|2≤x<3} -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
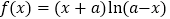 .
.(Ⅰ)当
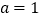 时,求曲线
时,求曲线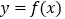 在
在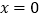 处的切线方程;
处的切线方程;(Ⅱ)当
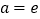 时,求证:函数
时,求证:函数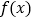 在
在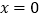 处取得最值.
处取得最值. -
科目: 来源: 题型:
查看答案和解析>>【题目】集合A={x|x2﹣3x﹣4<0,x∈Z}用列举法表示为
相关试题

