【题目】某研究小组在电脑上进行人工降雨模拟实验,准备用![]() 、
、![]() 、
、![]() 三种人工降雨方式分别对甲、乙、丙三地实施人工降雨,其试验数据统计如表:
三种人工降雨方式分别对甲、乙、丙三地实施人工降雨,其试验数据统计如表:
方式 | 实施地点 | 大雨 | 中雨 | 小雨 | 模拟实验总次数 |
| 甲 | 4次 | 6次 | 2次 | 12次 |
| 乙 | 3次 | 6次 | 3次 | 12次 |
| 丙 | 2次 | 2次 | 8次 | 12次 |
假定对甲、乙、丙三地实施的人工降雨彼此互不影响,请你根据人工降雨模拟实验的统计数据:
(Ⅰ)求甲、乙、丙三地都恰为中雨的概率;
(Ⅱ)考虑到旱情和水土流失,如果甲地恰需中雨即达到理想状态,乙地必须是大雨才达到理想状态,丙地只能是小雨或中雨即达到理想状态,记“甲、乙、丙三地中达到理想状态的个数”为随机变量![]() ,求随机变量
,求随机变量![]() 的分布列和数学期望
的分布列和数学期望![]() .
.
参考答案:
【答案】(1)![]() ;(2)分布列见解析,数学期望
;(2)分布列见解析,数学期望![]() .
.
【解析】试题分析:(1)由人工降雨模拟实验的统计数据,用![]() 、
、![]() 、
、![]() 三种人工降雨方式分别对甲、乙、丙三地实施人工降雨,求出大雨、中雨、小雨的概率分布表,再利用相互独立事件概率计算公式求出三地都为中雨的概率;(2)
三种人工降雨方式分别对甲、乙、丙三地实施人工降雨,求出大雨、中雨、小雨的概率分布表,再利用相互独立事件概率计算公式求出三地都为中雨的概率;(2)![]() 的可能取值为
的可能取值为![]() ,
,![]() ,
,![]() ,
,![]() ,分别求出
,分别求出![]() 取这几个值时的概率,再求出分布列和数学期望.
取这几个值时的概率,再求出分布列和数学期望.
试题解析:(1)由人工降雨模拟实验的统计数据,用![]() 、
、![]() 、
、![]() 三种人工降雨方式分别对甲、乙、丙三地实施人工降雨,得到大雨、中雨、小雨的概率如下表:
三种人工降雨方式分别对甲、乙、丙三地实施人工降雨,得到大雨、中雨、小雨的概率如下表:
方式 | 实施地点 | 大雨 | 中雨 | 小雨 |
| 甲 |
|
|
|
| 乙 |
|
|
|
| 丙 |
|
|
|
记“甲、乙、丙三地都恰为中雨”为事件![]() ,则
,则
![]() .
.
(2)设甲、乙、丙三地达到理想状态的概率分别为![]() 、
、![]() 、
、![]() ,
,
则![]() ,
,![]() ,
,![]() ,
,
![]() 的可能取值为0,1,2,3,
的可能取值为0,1,2,3,
![]() ;
;
![]()
![]() ;
;
![]()
![]() ;
;
![]() .
.
所以随机变量![]() 的分布列为:
的分布列为:
| 0 | 1 | 2 | 3 |
|
|
|
|
|
数学期望![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了完成对某城市的工薪阶层是否赞成调整个人所得税税率的调查,随机抽取了60人,作出了他们的月收入频率分布直方图(如图),同时得到了他们月收入情况与赞成人数统计表(如下表):
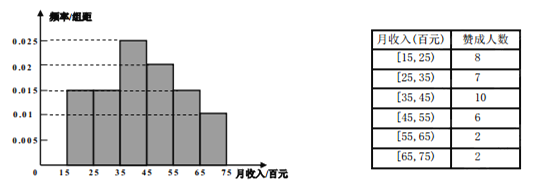
(1)试根据频率分布直方图估计这60人的平均月收入;
(2)若从月收入(单位:百元)在[65,75)的被调查者中随机选取2人进行追踪调查,求2人都不赞成的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆C的两个焦点分别为
 ,且椭圆C过点P(3,2).
,且椭圆C过点P(3,2).(Ⅰ)求椭圆C的标准方程;
(Ⅱ)与直线OP平行的直线交椭圆C于A,B两点,求△PAB面积的最大值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线
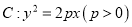 的焦点为
的焦点为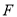 ,抛物线上横坐标为
,抛物线上横坐标为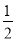 的点到抛物线顶点的距离与该点到抛物线准线的距离相等。
的点到抛物线顶点的距离与该点到抛物线准线的距离相等。(1)求抛物线
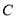 的方程;
的方程;(2)设直线
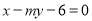 与抛物线
与抛物线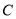 交于
交于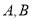 两点,若
两点,若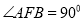 ,求实数
,求实数 的值。
的值。 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知数据x1,x2,x3,…,xn是普通职工n(n≥3,n∈N*)个人的年收入,设这n个数据的中位数为x,平均数为y,方差为z,如果再加上世界首富的年收入xn+1,则这n+1个数据中,下列说法正确的是
A. 年收入平均数大大增大,中位数一定变大,方差可能不变
B. 年收入平均数大大增大,中位数可能不变,方差变大
C. 年收入平均数大大增大,中位数可能不变,方差也不变
D. 年收入平均数可能不变,中位数可能不变,方差可能不变
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
 :
: 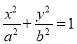 (
(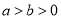 )的左焦点为
)的左焦点为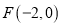 ,离心率为
,离心率为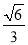 .
.(Ⅰ)求椭圆
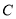 的标准方程;
的标准方程;(Ⅱ)设
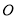 为坐标原点,
为坐标原点, 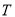 为直线
为直线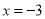 上一点,过
上一点,过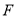 作
作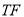 的垂线交椭圆于
的垂线交椭圆于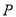 ,
, 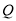 .当四边形
.当四边形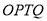 是平行四边形时,求四边形
是平行四边形时,求四边形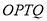 的面积。
的面积。 -
科目: 来源: 题型:
查看答案和解析>>【题目】某商店计划每天购进某商品若干件,商店每销售1件该商品可获利50元.若供大于求,剩余商品全部退回,则每件商品亏损10元;若供不应求,则从外部调剂,此时每件调剂商品可获利30元.
(Ⅰ)若商店一天购进该商品10件,求当天的利润y(单位:元)关于当天需求量n(单位:件,n∈N)的函数解析式;
(Ⅱ)商店记录了50天该商品的日需求量(单位:件),整理得下表:
日需求量n
8
9
10
11
12
频数
10
10
15
10
5
①假设该店在这50天内每天购进10件该商品,求这50天的日利润(单位:元)的平均数;
②若该店一天购进10件该商品,记“当天的利润在区间
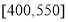 ”为事件A,求P(A)的估计值.
”为事件A,求P(A)的估计值.
相关试题

