【题目】如图,ABCD是边长为3的正方形,DE⊥平面ABCD,AF∥DE,DE=3AF,BE与平面ABCD所成角为60°. 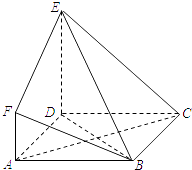
(1)求证:AC⊥平面BDE;
(2)设点M是线段BD上一个动点,试确定点M的位置,使得AM∥平面BEF,并证明你的结论.
参考答案:
【答案】
(1)证明:因为DE⊥平面ABCD,
所以DE⊥AC.
因为ABCD是正方形,
所以AC⊥BD,因为DE∩BD=D
从而AC⊥平面BDE.
(2)解:当M是BD的一个三等分点,即3BM=BD时,AM∥平面BEF.
取BE上的三等分点N,使3BN=BE,连接MN,NF,则DE∥MN,且DE=3MN,
因为AF∥DE,且DE=3AF,所以AF∥MN,且AF=MN,
故四边形AMNF是平行四边形.
所以AM∥FN,
因为AM平面BEF,FN平面BEF,
所以AM∥平面BEF.
【解析】(1)根据DE⊥平面ABCD,由线面垂直的判定定理可知DE⊥AC,由ABCD是正方形可知AC⊥BD,而DE∩BD=D,满足线面垂直的判定所需条件,从而证得结论;(2)当M是BD的一个三等分点,即3BM=BD时,AM∥平面BEF.取BE上的三等分点N,使3BN=BE,连接MN,NF,则DE∥MN,且DE=3MN,而AF∥DE,且DE=3AF,则四边形AMNF是平行四边形,从而AM∥FN,AM平面BEF,FN平面BEF,满足线面平行的判定定理,从而证得结论.
【考点精析】本题主要考查了直线与平面平行的判定和直线与平面垂直的判定的相关知识点,需要掌握平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行;一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直;注意点:a)定理中的“两条相交直线”这一条件不可忽视;b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在同一平面内,点P位于两平行直线l1、l2两侧,且P到l1 , l2的距离分别为1,3,点M,N分别在l1 , l2上,|
 +
+  |=8,则
|=8,则 
 的最大值为( )
的最大值为( ) 
A.15
B.12
C.10
D.9 -
科目: 来源: 题型:
查看答案和解析>>【题目】如下图所示,ABCD是边长为3的正方形,DE⊥平面ABCD,AF∥DE,DE=3AF,BE与平面ABCD所成的角为60°.

(1)求证:AC⊥平面BDE;
(2)求二面角F-BE-D的余弦值;
(3)设点M是线段BD上一个动点,试确定点M的位置,使得AM∥平面BEF,并证明你的结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于下列命题: ①在△ABC中,若sin2A=sin2B,则△ABC为等腰三角形;
②已知a,b,c是△ABC的三边长,若a=2,b=5, ,则△ABC有两组解;
,则△ABC有两组解;
③设 ,
,  ,
,  ,则a>b>c;
,则a>b>c;
④将函数 图象向左平移
图象向左平移  个单位,得到函数
个单位,得到函数  图象.
图象.
其中正确命题的序号是 . -
科目: 来源: 题型:
查看答案和解析>>【题目】一辆赛车在一个周长为
 的封闭跑道上行驶,跑道由几段直道和弯道组成,图
的封闭跑道上行驶,跑道由几段直道和弯道组成,图 反映了赛车在“计时赛”整个第二圈的行驶速度与行驶路程之间的关系.
反映了赛车在“计时赛”整个第二圈的行驶速度与行驶路程之间的关系.
图1

图2
根据图
 有以下四个说法:
有以下四个说法:①在这第二圈的
 到
到 之间,赛车速度逐渐增加;
之间,赛车速度逐渐增加;②在整个跑道中,最长的直线路程不超过
 ;
;③大约在这第二圈的
 到
到 之间,赛车开始了那段最长直线路程的行驶;
之间,赛车开始了那段最长直线路程的行驶;④在图
 的四条曲线(注:
的四条曲线(注: 为初始记录数据位置)中,曲线
为初始记录数据位置)中,曲线 最能符合赛车的运动轨迹.
最能符合赛车的运动轨迹.其中,所有正确说法的序号是( )
A. ①②③ B. ②③ C. ①④ D. ③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】
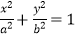 (a>b>0)如图,已知椭圆C:的左、右焦点分别为F1、F2 , 离心率为
(a>b>0)如图,已知椭圆C:的左、右焦点分别为F1、F2 , 离心率为 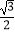 ,点A是椭圆上任一点,△AF1F2的周长为
,点A是椭圆上任一点,△AF1F2的周长为 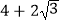 . (Ⅰ)求椭圆C的方程;
. (Ⅰ)求椭圆C的方程;
(Ⅱ)过点Q(﹣4,0)任作一动直线l交椭圆C于M,N两点,记 ,若在线段MN上取一点R,使得
,若在线段MN上取一点R,使得 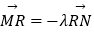 ,则当直线l转动时,点R在某一定直线上运动,求该定直线的方程.
,则当直线l转动时,点R在某一定直线上运动,求该定直线的方程.
-
科目: 来源: 题型:
查看答案和解析>>【题目】 ①求平行于直线3x+4y-12=0,且与它的距离是7的直线的方程;
②求垂直于直线x+3y-5="0," 且与点P(-1,0)的距离是
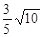 的直线的方程.
的直线的方程.
相关试题

