【题目】关于![]() 的方程
的方程![]() 的解集中只含有一个元素,则
的解集中只含有一个元素,则![]() 的取值集合为______.
的取值集合为______.
参考答案:
【答案】![]()
【解析】
先根据分式方程去分母得一元二次方程,再根据已知条件得出该一元二次方程的判别式和根的情况,得到关于![]() 的方程,求解可得
的方程,求解可得![]() 的取值集合.
的取值集合.
对关于![]() 的方程
的方程![]() 去分母,得
去分母,得![]() ,要使关于
,要使关于![]() 的方程
的方程![]() 的解集中只含有一个元素,
的解集中只含有一个元素,
则方程![]() 有两个相等的实数根,且该根不等于2,或者方程
有两个相等的实数根,且该根不等于2,或者方程![]() 有两个不等的实数根,且这两根中只有一个根是0或是2,
有两个不等的实数根,且这两根中只有一个根是0或是2,
当方程![]() 有两个相等的实数根,且该根不等于2,此时
有两个相等的实数根,且该根不等于2,此时![]() ,解得
,解得![]() ,经检验得此时方程的根不等于2;所以
,经检验得此时方程的根不等于2;所以![]() 满足题意;
满足题意;
当方程![]() 有两个不等的实数根,且这两根中只有一个根是0或是2,此时
有两个不等的实数根,且这两根中只有一个根是0或是2,此时![]() ,解得
,解得![]() ,当方程
,当方程![]() 的根为0时,即
的根为0时,即![]() ,解得
,解得![]() ,满足
,满足![]() ;当方程
;当方程![]() 的根为2时,即
的根为2时,即![]() ,解得
,解得![]() ,满足
,满足![]() ,
,
综上可得:![]() 的取值集合为
的取值集合为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】近年来,太阳能技术运用的步伐日益加快.2002年全球太阳能电池的年生产量达到670 MW,年生产量的增长率为34%.以后四年中,年生产量的增长率逐年递增2%(如,2003年的年生产量的增长率为36%).
(1)求2006年全球太阳能电池的年生产量(结果精确到0.1 MW);
(2)目前太阳能电池产业存在的主要问题是市场安装量远小于生产量,2006年的实际安装量为1420MW.假设以后若干年内太阳能电池的年生产量的增长率保持在42%,到2010年,要使年安装量与年生产量基本持平(即年安装量不少于年生产量的95%),这四年中太阳能电池的年安装量的平均增长率至少应达到多少(结果精确到0.1%)?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在正方体
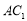 中,
中,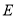 、
、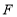 分别为
分别为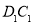 、
、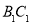 的中点,
的中点,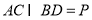 ,
,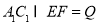 ,如图.
,如图.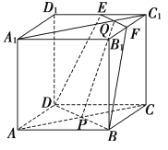
(1)若
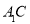 交平面
交平面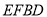 于点
于点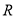 ,证明:
,证明: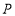 、
、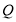 、
、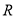 三点共线;
三点共线;(2)线段
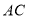 上是否存在点
上是否存在点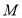 ,使得平面
,使得平面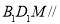 平面
平面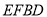 ,若存在确定
,若存在确定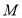 的位置,若不存在说明理由.
的位置,若不存在说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直四棱柱
 的底面是直角梯形,
的底面是直角梯形,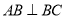 ,
,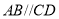 ,
,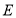 、
、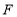 分别是棱
分别是棱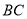 、
、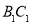 上的动点,且
上的动点,且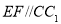 ,
,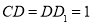 ,
,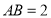 ,
,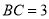 .
.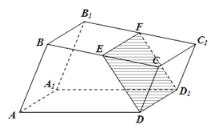
(1)证明:无论点
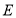 怎样运动,四边形
怎样运动,四边形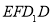 都为矩形;
都为矩形;(2)当
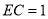 时,求几何体
时,求几何体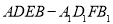 的体积.
的体积. -
科目: 来源: 题型:
查看答案和解析>>【题目】深受广大球迷喜爱的某支欧洲足球队.在对球员的使用上总是进行数据分析,为了考察甲球员对球队的贡献,现作如下数据统计:
球队胜
球队负
总计
甲参加



甲未参加



总计



(1)求
 的值,据此能否有
的值,据此能否有 的把握认为球队胜利与甲球员参赛有关;
的把握认为球队胜利与甲球员参赛有关;(2)根据以往的数据统计,乙球员能够胜任前锋、中锋、后卫以及守门员四个位置,且出场率分别为:
 ,当出任前锋、中锋、后卫以及守门员时,球队输球的概率依次为:
,当出任前锋、中锋、后卫以及守门员时,球队输球的概率依次为: .则:
.则:1)当他参加比赛时,求球队某场比赛输球的概率;
2)当他参加比赛时,在球队输了某场比赛的条件下,求乙球员担当前锋的概率;
3)如果你是教练员,应用概率统计有关知识.该如何使用乙球员?
附表及公式:
















 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知四棱锥
 中,底面
中,底面 为平行四边形,点
为平行四边形,点 、
、 、
、 分别在
分别在 、
、 、
、 上.
上.
(1)若
 ,求证:平面
,求证:平面 平面
平面 ;
;(2)若
 满足
满足 ,则
,则 点满足什么条件时,
点满足什么条件时, 面
面 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】为了解全市统考情况,从所有参加考试的考生中抽取4000名考生的成绩,频率分布直方图如下图所示.

(1)求这4000名考生的半均成绩
 (同一组中数据用该组区间中点作代表);
(同一组中数据用该组区间中点作代表);(2)由直方图可认为考生考试成绩z服从正态分布
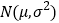 ,其中
,其中 分别取考生的平均成绩
分别取考生的平均成绩 和考生成绩的方差
和考生成绩的方差 ,那么抽取的4000名考生成绩超过84.81分(含84.81分)的人数估计有多少人?
,那么抽取的4000名考生成绩超过84.81分(含84.81分)的人数估计有多少人?(3)如果用抽取的考生成绩的情况来估计全市考生的成绩情况,现从全市考生中随机抽取4名考生,记成绩不超过84.81分的考生人数为
 ,求
,求 .(精确到0.001)
.(精确到0.001)附:①
 ;
;②
 ,则
,则 ;
;③
 .
.
相关试题

