【题目】已知f(x)= ![]() (ax﹣a﹣x)(a>0且a≠1).
(ax﹣a﹣x)(a>0且a≠1).
(1)判断f(x)的奇偶性.
(2)讨论f(x)的单调性.
(3)当x∈[﹣1,1]时,f(x)≥b恒成立,求b的取值范围.
参考答案:
【答案】
(1)解:∵f(x)= ![]() ,
,
所以f(x)定义域为R,
又f(﹣x)= ![]() (a﹣x﹣ax)=﹣
(a﹣x﹣ax)=﹣ ![]() (ax﹣a﹣x)=﹣f(x),
(ax﹣a﹣x)=﹣f(x),
所以函数f(x)为奇函数
(2)解:任取x1<x2
则f(x2)﹣f(x1)= ![]() (ax2﹣ax1)(1+a﹣(x1+x2))
(ax2﹣ax1)(1+a﹣(x1+x2))
∵x1<x2,且a>0且a≠1,1+a﹣(x1+x2)>0
①当a>1时,a2﹣1>0,ax2﹣ax1>0,则有f(x2)﹣f(x1)>0,
②当0<a<1时,a2﹣1<0.,ax2﹣ax1<0,则有f(x2)﹣f(x1)>0,
所以f(x)为增函数
(3)解:当x∈[﹣1,1]时,f(x)≥b恒成立,
即b小于等于f(x)的最小值,
由(2)知当x=﹣1时,f(x)取得最小值,最小值为 ![]() (
( ![]() )=﹣1,
)=﹣1,
∴b≤﹣1.
求b的取值范围(﹣∞,﹣1]
【解析】(1)由函数的解析式可求函数的定义域,先证奇偶性:代入可得f(﹣x)=﹣f(x),从而可得函数为奇函数;(2)再证单调性:利用定义任取x1<x2 , 利用作差比较f(x1)﹣f(x2)的正负,从而确当f(x1)与f(x2)的大小,进而判断函数的单调性;(3)对一切x∈[﹣1,1]恒成立,转化为b小于等于f(x)的最小值,利用(2)的结论求其最小值,从而建立不等关系解之即可.
【考点精析】根据题目的已知条件,利用函数的奇偶性的相关知识可以得到问题的答案,需要掌握偶函数的图象关于y轴对称;奇函数的图象关于原点对称.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知f(x)为定义在[﹣1,1]上的奇函数,当x∈[﹣1,0]时,函数解析式f(x)=
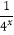 ﹣
﹣ 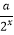 (a∈R).
(a∈R).
(1)写出f(x)在[0,1]上的解析式;
(2)求f(x)在[0,1]上的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】甲乙丙三人在进行一项投掷骰子游戏中规定:若掷出1点,甲得1分,若掷出2点或3点,乙得1分;若掷出4点或5点或6点,丙得1分,前后共掷3次,设x,y,z分别表示甲、乙、丙三人的得分.
(1)求x=0,y=1,z=2的概率;
(2)记ξ=x+z,求随机变量ξ的概率分布列和数学期望. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=﹣x3+ax2+1,(a∈R).
(1)若f(x)图象上横坐标为1的点处存在垂直于y轴的切线,求a的值;
(2)若f(x)在区间(﹣1,2)内有两个不同的极值点,求a取值范围;
(3)当a=1时,是否存在实数m,使得函数g(x)=x4﹣5x3+(2﹣m)x2+1的图象于函数f(x)的图象恰有三个不同的交点,若存在,试求出实数m的值;若不存在,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列
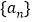 的前
的前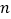 项和为
项和为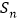 ,
,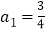 ,
,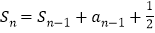 (
(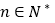 且
且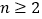 ),数列
),数列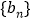 满足:
满足: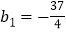 ,且
,且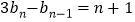 (
(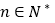 且
且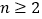 ).
).(Ⅰ)求数列
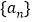 的通项公式;
的通项公式;(Ⅱ)求证:数列
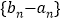 为等比数列;
为等比数列;(Ⅲ)求数列
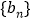 的前
的前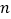 项和的最小值.
项和的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】设
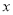 ,
, 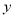 满足约束条件
满足约束条件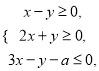 若目标函数
若目标函数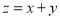 的最小值为
的最小值为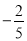 ,则实数
,则实数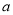 的值为
的值为A.
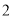 B.
B. 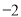 C.
C. 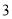 D.
D. 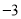
-
科目: 来源: 题型:
查看答案和解析>>【题目】函数f(x)=ln
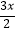 ﹣
﹣ 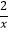 的零点一定位于区间( )
的零点一定位于区间( )
A.(1,2)
B.(2,3)
C.(3,4)
D.(4,5)
相关试题

