【题目】已知数列![]() 的前
的前![]() 项和为
项和为![]() ,
,![]() ,
,![]() (
(![]() 且
且![]() ),数列
),数列![]() 满足:
满足:![]() ,且
,且![]() (
(![]() 且
且![]() ).
).
(Ⅰ)求数列![]() 的通项公式;
的通项公式;
(Ⅱ)求证:数列![]() 为等比数列;
为等比数列;
(Ⅲ)求数列![]() 的前
的前![]() 项和的最小值.
项和的最小值.
参考答案:
【答案】(1)![]() (2)见解析(3)
(2)见解析(3)![]()
【解析】试题分析:(1)由![]() 得
得![]() ,所以
,所以![]() 。(2)
。(2)![]()
![]()
![]()
![]() (
(![]() )
)![]()
![]()
![]() (
(![]() )
)
所以![]() (
(![]() )且
)且![]() 。所以得证。(3)
。所以得证。(3)
(Ⅱ)得![]() 所以
所以![]()
![]() ,所以
,所以![]() 是递增数列
是递增数列
和最小,即所有的负数项的和,只需求到![]() 。
。
试题解析:(Ⅰ)由![]() 得
得![]()
即![]() (
(![]() 且
且![]() )
)
则数列![]() 为以
为以![]() 为公差的等差数列
为公差的等差数列
因此![]()
![]()
(Ⅱ)证明:因为![]() (
(![]() )
)
所以![]() (
(![]() )
)
![]()
![]()
![]()
![]() (
(![]() )
)
![]()
![]()
![]() (
(![]() )
)
所以![]() (
(![]() )
)
因为![]()
所以数列![]() 是以
是以![]() 为首项,
为首项,![]() 为公比的等比数列.
为公比的等比数列.
(Ⅲ)由(Ⅱ)得![]()
所以![]()
![]()
![]()
![]()
![]()
![]() (
(![]() )
)
所以![]() 是递增数列.
是递增数列.
因为当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]()
当![]() 时,
时,![]()
所以数列![]() 从第3项起的各项均大于0,故数列
从第3项起的各项均大于0,故数列![]() 的前2项之和最小.
的前2项之和最小.
记数列![]() 的前
的前![]() 项和为
项和为![]() ,则
,则![]()
![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲乙丙三人在进行一项投掷骰子游戏中规定:若掷出1点,甲得1分,若掷出2点或3点,乙得1分;若掷出4点或5点或6点,丙得1分,前后共掷3次,设x,y,z分别表示甲、乙、丙三人的得分.
(1)求x=0,y=1,z=2的概率;
(2)记ξ=x+z,求随机变量ξ的概率分布列和数学期望. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=﹣x3+ax2+1,(a∈R).
(1)若f(x)图象上横坐标为1的点处存在垂直于y轴的切线,求a的值;
(2)若f(x)在区间(﹣1,2)内有两个不同的极值点,求a取值范围;
(3)当a=1时,是否存在实数m,使得函数g(x)=x4﹣5x3+(2﹣m)x2+1的图象于函数f(x)的图象恰有三个不同的交点,若存在,试求出实数m的值;若不存在,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知f(x)=
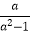 (ax﹣a﹣x)(a>0且a≠1).
(ax﹣a﹣x)(a>0且a≠1).
(1)判断f(x)的奇偶性.
(2)讨论f(x)的单调性.
(3)当x∈[﹣1,1]时,f(x)≥b恒成立,求b的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】设
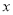 ,
, 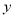 满足约束条件
满足约束条件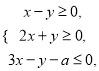 若目标函数
若目标函数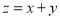 的最小值为
的最小值为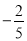 ,则实数
,则实数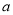 的值为
的值为A.
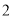 B.
B. 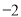 C.
C. 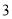 D.
D. 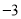
-
科目: 来源: 题型:
查看答案和解析>>【题目】函数f(x)=ln
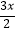 ﹣
﹣ 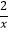 的零点一定位于区间( )
的零点一定位于区间( )
A.(1,2)
B.(2,3)
C.(3,4)
D.(4,5) -
科目: 来源: 题型:
查看答案和解析>>【题目】下列表示错误的是( )
A.0??
B.??{1,2}
C.{(x,y)|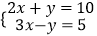 ={3,4}
={3,4}
D.若A?B,则A∩B=A
相关试题

