【题目】已知函数![]() ,
, ![]() ,
, ![]() .
.
(1)当![]() 时,求
时,求![]() 的极值;
的极值;
(2)令![]() ,求函数
,求函数![]() 的单调减区间.
的单调减区间.
参考答案:
【答案】(1)当![]() 时,
时, ![]() 取极大值
取极大值![]() ;(2)详见解析.
;(2)详见解析.
【解析】试题分析:(1)将a=0代入,求出f(x)的导数,从而求出函数的极值;(2)先求出
h(x)的导数,通过讨论a的范围,从而求出函数的递减区间.
试题解析:
(1)当![]() 时,
时, ![]() ,故
,故![]() (
(![]() )
)
当![]() 时,
时, ![]() ,
, ![]() 单调递增;
单调递增;
当![]() 时,
时, ![]() ,
, ![]() 单调递减;
单调递减;
故当![]() 时,
时, ![]() 取极大值
取极大值![]() .
.
(2)![]()
![]() ,令
,令![]() 得
得![]() ,
, ![]() ,
,
若![]() ,由
,由![]() 得
得![]() ,
, ![]() 的单调减区间为
的单调减区间为![]() ;
;
若![]() ,①当
,①当![]() 时,
时, ![]() ,由
,由![]() 得
得![]() ,或
,或![]() ,
,
所以![]() 的单调减区间为
的单调减区间为![]() ,
, ![]() ;
;
②当![]() 时,总有
时,总有![]() ,故
,故![]() 的单调减区间为
的单调减区间为![]() ;
;
③当![]() 时,
时, ![]() ,由
,由![]() 得
得![]() ,或
,或![]() ,
,
所以![]() 的单调减区间为
的单调减区间为![]() ,
, ![]() ;
;
综上所述,当![]() ,
, ![]() 的单调减区间为
的单调减区间为![]() ,
, ![]() ;
;
当![]() 时,
时, ![]() 的单调减区间为
的单调减区间为![]() ;
;
当![]() 时,
时, ![]() 的单调减区间为
的单调减区间为![]() ,
, ![]() ;
;
当![]() 时,
时, ![]() 的单调减区间为
的单调减区间为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在直角坐标系中,以原点为极点,x轴的正半轴为极轴建立极坐标系,已知曲线C:ρsin2θ=2acos θ(a>0),过点P(-2,-4)的直线l:
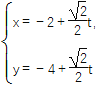 (t为参数)与曲线C相交于M,N两点.
(t为参数)与曲线C相交于M,N两点.(1)求曲线C的直角坐标方程和直线l的普通方程;
(2)若|PM|,|MN|,|PN|成等比数列,求实数a的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设函数
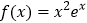 .
.(Ⅰ)求曲线
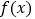 在点
在点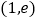 处的切线方程;
处的切线方程;(Ⅱ)若
 对
对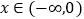 恒成立,求实数
恒成立,求实数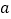 的取值范围;
的取值范围;(Ⅲ)求整数
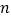 的值,使函数
的值,使函数 在区间
在区间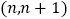 上有零点.
上有零点. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆C:x2+y2=4,直线l:x+y=2.以O为极点,x轴的正半轴为极轴,取相同的单位长度建立极坐标系.
(1)将圆C和直线l的方程化为极坐标方程;
(2)P是l上的点,射线OP交圆C于点R,又点Q在OP上且满足|OQ|·|OP|=|OR|2,当点P在l上移动时,求点Q轨迹的极坐标方程.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
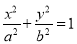 (
(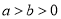 )的离心率为
)的离心率为 ,短轴的一个端点为
,短轴的一个端点为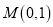 .过椭圆左顶点
.过椭圆左顶点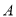 的直线
的直线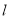 与椭圆的另一交点为
与椭圆的另一交点为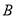 .
.(1)求椭圆的方程;
(2)若
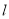 与直线
与直线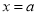 交于点
交于点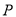 ,求
,求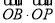 的值;
的值;(3)若
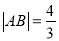 ,求直线
,求直线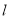 的倾斜角.
的倾斜角. -
科目: 来源: 题型:
查看答案和解析>>【题目】在直角坐标系xOy中,以O为极点,x轴正半轴为极轴建立极坐标系,直线l的参数方程为
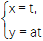 (t为参数),曲线C1的方程为ρ(ρ-4sin θ)=12,定点A(6,0),点P是曲线C1上的动点,Q为AP的中点.
(t为参数),曲线C1的方程为ρ(ρ-4sin θ)=12,定点A(6,0),点P是曲线C1上的动点,Q为AP的中点.(1)求点Q的轨迹C2的直角坐标方程;
(2)直线l与直线C2交于A,B两点,若|AB|≥2
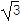 ,求实数a的取值范围.
,求实数a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,过点
 的直线与圆
的直线与圆 相交于
相交于 两点,过点
两点,过点 且与
且与 垂直的直线与圆
垂直的直线与圆 的另一交点为
的另一交点为 .
.
(1)当点
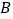 坐标为
坐标为 时,求直线
时,求直线 的方程;
的方程;(2)求四边形
 面积
面积 的最大值.
的最大值.
相关试题

