【题目】甲、乙两家外卖公司,其送餐员的日工资方案如下:甲公司的底薪80元,每单抽成4元;乙公司无底薪,40单以内(含40单)的部分每单抽成6元,超出40单的部分每单抽成7元,假设同一公司送餐员一天的送餐单数相同,现从两家公司各随机抽取一名送餐员,并分别记录其50天的送餐单数,得到如下频数表:
甲公司送餐员送餐单数频数表
送餐单数 | 38 | 39 | 40 | 41 | 42 |
天数 | 10 | 15 | 10 | 10 | 5 |
乙公司送餐员送餐单数频数表
送餐单数 | 38 | 39 | 40 | 41 | 42 |
天数 | 5 | 10 | 10 | 20 | 5 |
(1)现从甲公司记录的50天中随机抽取3天,求这3天送餐单数都不小于40的概率;
(2)若将频率视为概率,回答下列两个问题:
①记乙公司送餐员日工资为![]() (单位:元),求
(单位:元),求![]() 的分布列和数学期望;
的分布列和数学期望;
②小王打算到甲、乙两家公司中的一家应聘送餐员,如果仅从日工资的角度考虑,请利用所学的统计学知识为小王作出选择,并说明理由.
参考答案:
【答案】(1)![]() .(2)见解析
.(2)见解析
【解析】试题分析:(1)为古典概型,利用组合数公式计算基本事件的总数和随机事件中含有的基本事件的总数即可.(2)为计算离散型随机变量的分布列和数学期望,利用公式计算即可.
(1)记抽取的![]() 天送餐单数都不小于40为事件
天送餐单数都不小于40为事件![]() ,则
,则![]() .
.
(2)①设乙公司送餐员送餐单数为![]() ,
,
则当![]() 时,
时, ![]() ,当
,当![]() 时,
时, ![]() ,当
,当![]() 时,
时, ![]() ,当
,当![]() 时,
时, ![]() ,当
,当![]() 时,
时, ![]() .
.
所以![]() 的所有可能取值为228,234,240,247,254.故
的所有可能取值为228,234,240,247,254.故![]() 的分布列为:
的分布列为:
| 228 | 234 | 240 | 247 | 254 |
|
|
|
|
|
|
所以![]()
②依题意,甲公司送餐员日平均送餐单数为![]()
所以甲公司送餐员日平均工资为![]() 元.
元.
由①得乙公司送餐员日平均工资为241.8元.因为![]() ,故推荐小王去乙公司应聘.
,故推荐小王去乙公司应聘.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某花店每天以每枝
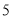 元的价格从农场购进若干枝玫瑰花,然后以每枝
元的价格从农场购进若干枝玫瑰花,然后以每枝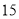 元的价格出售.如果当天卖不完,剩下的玫瑰花做垃圾处理.
元的价格出售.如果当天卖不完,剩下的玫瑰花做垃圾处理.(1)若花店一天购进
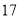 枝玫瑰花,求当天的利润
枝玫瑰花,求当天的利润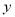 (单位:元)关于当天需求量
(单位:元)关于当天需求量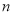 (单位:枝,
(单位:枝, 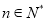 )的函数解析式.
)的函数解析式.(2)花店记录了
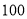 天玫瑰花的日需求量(单位:枝),整理得下表:
天玫瑰花的日需求量(单位:枝),整理得下表:日需求量
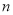
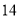
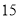
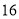
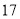
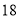
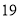
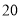
频数
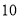
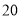
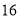
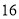
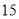
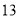
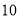
假设花店在这
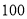 天内每天购进
天内每天购进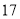 枝玫瑰花,求这
枝玫瑰花,求这 天的日利润(单位:元)的平均数.
天的日利润(单位:元)的平均数. -
科目: 来源: 题型:
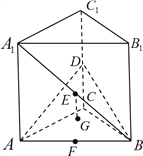
查看答案和解析>>【题目】如图,在直三棱柱
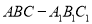 中,底面是等腰直角三角形,
中,底面是等腰直角三角形, 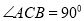 ,侧棱
,侧棱 ,点
,点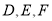 分别为棱
分别为棱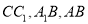 的中点,
的中点, 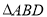 的重心为
的重心为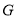 ,直线
,直线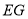 垂直于平面
垂直于平面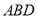 .
.
(1)求证:直线
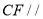 平面
平面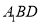 ;
;(2)求二面角
 的余弦.
的余弦. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
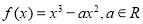 .
.(1)若
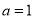 ,求曲线在
,求曲线在 点处的切线方程;
点处的切线方程;(2)若曲线
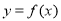 与直线
与直线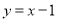 只有一个交点,求实数
只有一个交点,求实数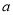 的取值范围.
的取值范围. -
科目: 来源: 题型:
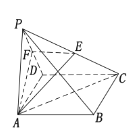
查看答案和解析>>【题目】如图,在四棱锥
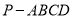 中,
中, 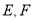 分别是
分别是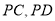 的中点,底面
的中点,底面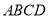 是边长为2的正方形,
是边长为2的正方形, 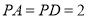 ,且平面
,且平面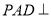 平面
平面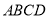 .
.
(1)求证:平面
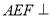 平面
平面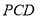 ;
;(2)求平面
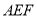 与平面
与平面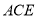 所成锐二面角的余弦值.
所成锐二面角的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知短轴长为2的椭圆
 ,直线
,直线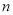 的横、纵截距分别为
的横、纵截距分别为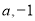 ,且原点到直线
,且原点到直线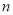 的距离为
的距离为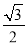 .
.(1)求椭圆
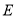 的方程;
的方程;(2)直线
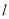 经过椭圆的右焦点
经过椭圆的右焦点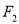 且与椭圆
且与椭圆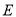 交于
交于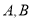 两点,若椭圆
两点,若椭圆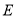 上存在一点
上存在一点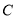 满足
满足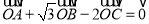 ,求直线
,求直线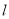 的方程.
的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
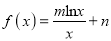 ,
, 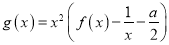 (
(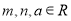 ),且曲线
),且曲线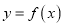 在点
在点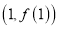 处的切线方程为
处的切线方程为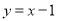 .
.(1)求实数
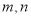 的值及函数
的值及函数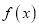 的最大值;
的最大值;(2)当
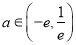 时,记函数
时,记函数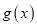 的最小值为
的最小值为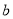 ,求
,求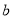 的取值范围.
的取值范围.
相关试题

