【题目】某项科研活动共进行了5次试验,其数据如下表所示:
特征量 | 第1次 | 第2次 | 第3次 | 第4次 | 第5次 |
| 555 | 559 | 551 | 563 | 552 |
| 601 | 605 | 597 | 599 | 598 |
(1)从5次特征量![]() 的试验数据中随机地抽取两个数据,求至少有一个大于600的概率;
的试验数据中随机地抽取两个数据,求至少有一个大于600的概率;
(2)求特征量![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;并预测当特征量
;并预测当特征量![]() 为570时特征量
为570时特征量![]() 的值.
的值.
(附:回归直线的斜率和截距的最小二乘法估计公式分别为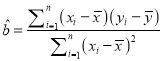 ,
, ![]() )
)
参考答案:
【答案】(1)![]() (2)线性回归方程为
(2)线性回归方程为![]() .当
.当![]() 时,特征量
时,特征量![]() 的估计值为
的估计值为![]() .
.
【解析】试题分析:(1)列举出基本事件共![]() 个,事件
个,事件![]() 的基本事件共7个,由古典概型计算公式,可得结论;(2)求出回归系数,即可求特征量
的基本事件共7个,由古典概型计算公式,可得结论;(2)求出回归系数,即可求特征量![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ,并预测当
,并预测当![]() 为
为![]() 时
时![]() 的值.
的值.
试题解析:(1)记“至少有一个大于600”为事件![]() .
.
基本事件有![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,共10个.
,共10个.
其中包含事件![]() 的基本事件有
的基本事件有![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,共7个.
,共7个.
∴![]() .
.
(2)![]() ,
, ![]() .
.
∴
∵![]() ,
,
∴线性回归方程为![]() .
.
当![]() 时,
时, ![]()
∴当![]() 时,特征量
时,特征量![]() 的估计值为
的估计值为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
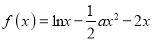
(1)若函数
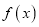 在定义域内单调递增,求实数
在定义域内单调递增,求实数 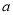 的取值范围,
的取值范围,(2)当
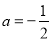 时,关于
时,关于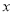 的方程
的方程 在[1,4]上恰有两个不相等的实数根,
在[1,4]上恰有两个不相等的实数根,求实数的取值范围。
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个盒子里装有三张卡片,分别标记有数字1,2,3,这三张卡片除标记的数字外完全相同.随机有放回地抽取3次,每次抽取1张,将抽取的卡片上的数字依次记为a,b,c.求:
(1)“抽取的卡片上的数字满足a+b=c”的概率;
(2)“抽取的卡片上的数字a,b,c不完全相同”的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了了解某地区心肺疾病是否与性别有关,在某医院随机地对入院
的50人进行了问卷调查,得到了如下的
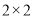 列联表:
列联表:患心肺疾病
不患心肺疾病
合计
男
20
5
25
女
10
15
25
合计
30
20
50
(1)用分层抽样的方法在患心肺疾病的人群中抽取6人,其中男性抽多少人?
(2)在上述抽取的6人中选2人,求恰有一名女性的概率;
(3)为了研究心肺疾病是否与性别有关,请计算出统计量
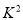 ,判断是否有
,判断是否有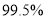 的把握认为
的把握认为患心肺疾病与性别有关?
右面的临界值表供参考:
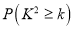
0.15
0.10
0.05
0.025
0.010
0.005
0.001
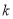
2.072
2.706
3.841
5.024
6.635
7.879
10.828
(参考公式:
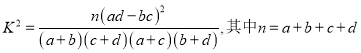 )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系
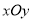 中,已知椭圆
中,已知椭圆 (
(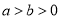 ),圆
),圆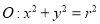 (
(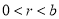 ),若圆
),若圆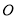 的一条切线
的一条切线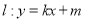 与椭圆
与椭圆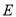 相交于
相交于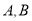 两点.
两点.(1)当
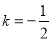 ,
, 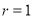 时,若点
时,若点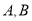 都在坐标轴的正半轴上,求椭圆
都在坐标轴的正半轴上,求椭圆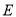 的方程;
的方程;(2)若以
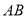 为直径的圆经过坐标原点
为直径的圆经过坐标原点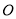 ,探究
,探究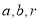 之间的等量关系,并说明理由.
之间的等量关系,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线
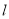 的参数方程为
的参数方程为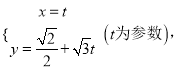 若以直角坐标系xOy的O点为极点,Ox方向为极轴,选择相同的长度单位建立极坐标系,得曲线C的极坐标方程为
若以直角坐标系xOy的O点为极点,Ox方向为极轴,选择相同的长度单位建立极坐标系,得曲线C的极坐标方程为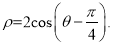
(1)求直线
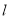 的斜率和曲线C的直角坐标方程;
的斜率和曲线C的直角坐标方程;(2)若直线
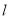 与曲线C交于A、B 两点,设点
与曲线C交于A、B 两点,设点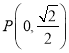 ,求|PA|+|PB|.
,求|PA|+|PB|. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=ex+ax-a(a∈R且a≠0)在点
 处的切线
处的切线与直线
 平行, (1)求实数a的值,
平行, (1)求实数a的值,(2)求此时f(x)在[-2,1]上的最大、最小值;
相关试题

