【题目】已知函数f(x)=2ax﹣2,g(x)=a(x﹣2a)(x+2﹣a),a∈R且a≠0.
(1)若{x|f(x)g(x)=0}={1,2},求实数a的值;
(2)若{x|f(x)<0或g(x)<0}=R,求实数a的取值范围.
参考答案:
【答案】
(1)解: ![]()
g(x)=a(x﹣2a)(x+a﹣2)=0得x=2a,x=2﹣a
∵{x|f(x)g(x)=0}={1,2},
∴ ![]()
经检验a=1符合题意,∴a=1
(2)解法1:设由于{x|f(x)<0或g(x)<0}=R
当a>0时,x→+∞总有f(x)>0,g(x)>0不符合题意
当a<0时,由f(x),g(x)的图象可得f(x)<0或g(x)<0成立则 ![]()
∴ ![]()
解法2:设由于{x|f(x)<0或g(x)<0}=R
当a>0时,x→+∞总有f(x)>0,g(x)>0不符合题意
当a<0时,若f(x)<0,则 ![]()
若g(x)<0,则x∈(2﹣a,+∞)∪(﹣∞,2a)
则 ![]()
∴ ![]()
综上 ![]()
【解析】(1)通过方程的根,结合已知条件求解即可.(2)解法1:利用{x|f(x)<0或g(x)<0}=R,通过当a>0时,当a<0时,结合函数的图象验证求解即可.解法2:由于{x|f(x)<0或g(x)<0}=R,验证当a>0时,不符合题意,当a<0时,讨论若f(x)<0,若g(x)<0,推出结果即可.
【考点精析】本题主要考查了函数的值的相关知识点,需要掌握函数值的求法:①配方法(二次或四次);②“判别式法”;③反函数法;④换元法;⑤不等式法;⑥函数的单调性法才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设集合A={x|ax2+bx+1=0}(a∈R,b∈R),集合B={﹣1,1}.
(1)若BA,求实数a的值;
(2)若A∩B≠,求a2﹣b2+2a的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】给出下列四个命题:
①“三个球全部放入两个盒子,其中必有一个盒子有一个以上的球”是必然事件
②“当x为某一实数时可使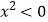 ”是不可能事件
”是不可能事件
③“明天顺德要下雨”是必然事件
④“从100个灯泡中取出5个,5个都是次品”是随机事件.
其中正确命题的个数是 ( )
A.0
B.1
C.2
D.3 -
科目: 来源: 题型:
查看答案和解析>>【题目】【2017庄河高级中学四模】如图,四棱锥
 中,底面
中,底面 是矩形,平面
是矩形,平面 平面
平面 ,且
,且 是边长为
是边长为 的等边三角形,
的等边三角形,  ,点
,点 是
是 的中点.
的中点.
(1)求证:
 平面
平面 ;
;(2)求四面体
 的体积.
的体积. -
科目: 来源: 题型:
查看答案和解析>>【题目】某学校研究性学习小组对该校高三学生视力情况进行调查,在高三的全体
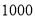 名学生中随机抽取了
名学生中随机抽取了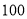 名学生的体检表,并得到如图的频率分布直方图.
名学生的体检表,并得到如图的频率分布直方图.年级名次
是否近视
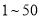

近视
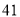
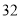
不近视
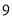
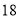
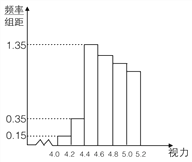
(1)若直方图中后四组的频数成等差数列,试估计全 年级视力在
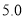 以下的人数;
以下的人数;(2)学习小组成员发现,学习成绩突出的学生,近视的比较多,为了研究学生的视力与学习成绩是否有关系,对年级名次在
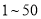 名和
名和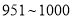 名的学生进行了调查,得到右表中数据,根据表中的数据,能否在犯错的概率不超过
名的学生进行了调查,得到右表中数据,根据表中的数据,能否在犯错的概率不超过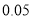 的前提下认为视力与学习成绩有关系?
的前提下认为视力与学习成绩有关系? 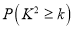
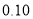
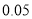

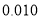
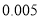
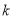


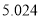
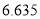
7.879

附:

-
科目: 来源: 题型:
查看答案和解析>>【题目】函数f(x)=﹣x2+(3﹣2m)x+2+m(0<m≤1).
(1)若x∈[0,m],证明:f(x)≤ ;
;
(2)求|f(x)|在[﹣1,1]上的最大值g(m). -
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆
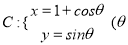 为参数
为参数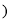 和直线
和直线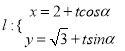
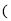 其中
其中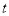 为参数,
为参数, 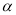 为直线
为直线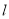 的倾斜角
的倾斜角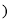 .
.(1)当
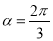 时,求圆上的点到直线
时,求圆上的点到直线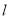 的距离的最小值;
的距离的最小值;(2)当直线
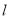 与圆
与圆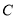 有公共点时,求
有公共点时,求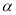 的取值范围.
的取值范围.
相关试题

