【题目】为了估计某自然保护区中天鹅的数量,可以使用以下方法:先从该保护区中捕出一定数量的天鹅,例如200只,给每只天鹅做上不影响其存活的记号,然后放回保护区,经过适当的时间,让其和保护区中其余的天鹅充分混合,再从保护区中捕出一定数量的天鹅,例如150只,查看其中有记号的天鹅,设有20只,试根据上述数据,估计该自然保护区中天鹅的数量.
参考答案:
【答案】1500只。
【解析】试题分析:根据频率等于频数除以总数得频率,再根据等可能性以频率估计概率,最后根据总数等于频数除以概率得结果
试题解析:设保护区中天鹅的数量约为n,假定每只天鹅被捕到的可能性是相等的,从保护区中任捕一只,设事件A={带有记号的天鹅},则P(A)=![]() ,第二次从保护区中捕出150只天鹅,其中有20只带有记号,由概率的统计定义可知P(A)=
,第二次从保护区中捕出150只天鹅,其中有20只带有记号,由概率的统计定义可知P(A)=![]() ,由两式,得
,由两式,得![]() ,解得n=1 500,
,解得n=1 500,
所以该自然保护区中天鹅的数量约为1 500只.
-
科目: 来源: 题型:
查看答案和解析>>【题目】三个臭皮匠顶上一个诸葛亮,能顶得上吗?在一次有关“三国演义”的知识竞赛中,三个臭皮匠A、B、C能答对题目的概率分别为P(A)=
 ,P(B)=
,P(B)= ,P(C)=
,P(C)= ,诸葛亮D能答对题目的概率为P(D)=
,诸葛亮D能答对题目的概率为P(D)= ,如果将三个臭皮匠A、B、C组成一组与诸葛亮D比赛,答对题目多者为胜方,问哪方胜?
,如果将三个臭皮匠A、B、C组成一组与诸葛亮D比赛,答对题目多者为胜方,问哪方胜? -
科目: 来源: 题型:
查看答案和解析>>【题目】海州市六一儿童节期间在妇女儿童活动中心举行小学生“海州杯”围棋比赛,规则如下:甲、乙两名选手比赛时,每局胜者得1分,负者得0分,比赛进行到有一人比对方多2分或赛满6局时比赛结束.设某校选手甲与另一选手乙比赛时,甲每局获胜的概率皆为
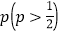 ,且各局比赛胜负互不影响,已知第二局比赛结束时比赛停止的概率为
,且各局比赛胜负互不影响,已知第二局比赛结束时比赛停止的概率为 .
.(1)求
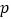 的值;
的值;(2)设
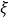 表示比赛停止时已比赛的局数,求随机变量
表示比赛停止时已比赛的局数,求随机变量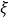 的分布列和数学期望
的分布列和数学期望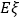 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
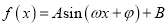 (
(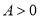 ,
, 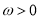 ,
, 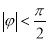 )的一系列对应最值如表:
)的一系列对应最值如表: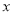
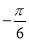
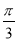
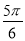
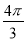
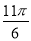
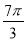
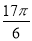
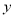
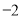
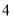
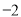
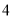
(1)根据表格提供的数据求函数
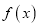 的解析式;
的解析式;(2)求函数
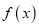 的单调递增区间和对称轴;
的单调递增区间和对称轴;(3)若当
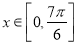 时,方程
时,方程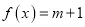 恰有两个不同的解,求实数
恰有两个不同的解,求实数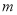 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】设人的某一特征(如眼睛的大小)是由他的一对基因所决定,以d表示显性基因,r表示隐性基因,则具有dd基因的人为纯显性,具有rr基因的人为纯隐性,具有rd基因的人为混合性,纯显性与混合性的人都显露显性基因决定的某一特征,孩子从父母身上各得到一个基因,假定父母都是混合性,问:
(1)1个孩子显露显性特征的概率是多少?
(2)“该父母生的2个孩子中至少有1个显露显性特征”,这种说法正确吗?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学从参加高一年级上学期期末考试的学生中抽出60名学生,将其成绩(均为整数)分成六段[40,50),[50,60),…,[90,100]后画出如下部分频率分布直方图.观察图形的信息,回答下列问题:
(1)估计这次考试的及格率(60分及以上为及格).
(2)从成绩是70分以上(包括70分)的学生中选一人,求选到第一名学生的概率(第一名学生只一人).

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点
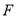 为椭圆
为椭圆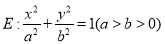 的左焦点,且两焦点与短轴的一个顶点构成一个等边三角形,直线
的左焦点,且两焦点与短轴的一个顶点构成一个等边三角形,直线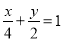 与椭圆
与椭圆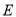 有且仅有一个交点
有且仅有一个交点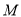 .
.(Ⅰ)求椭圆
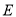 的方程;
的方程;(Ⅱ)设直线
 与
与 轴交于
轴交于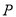 ,过点
,过点 的直线与椭圆
的直线与椭圆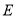 交于两不同点
交于两不同点 ,
, 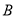 ,若
,若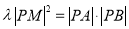 ,求实数
,求实数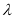 的取值范围.
的取值范围.
相关试题

