【题目】如图,几何体EF-ABCD中,四边形CDEF是正方形,四边形ABCD为直角梯形,AB∥CD,AD⊥DC,△ACB是腰长为2![]() 的等腰直角三角形,平面CDEF⊥平面ABCD.
的等腰直角三角形,平面CDEF⊥平面ABCD.
(1)求证:BC⊥AF;
(2)求几何体EF-ABCD的体积.

参考答案:
【答案】(1)详见解析;(2)![]() .
.
【解析】
(1)推导出FC⊥CD,FC⊥BC,AC⊥BC,由此BC⊥平面ACF,从而BC⊥AF.
(2)推导出AC=BC=2![]() ,AB
,AB![]() 4,从而AD=BCsin∠ABC=2
4,从而AD=BCsin∠ABC=2![]() 2,由V几何体EF﹣ABCD=V几何体A﹣CDEF+V几何体F﹣ACB,能求出几何体EF﹣ABCD的体积.
2,由V几何体EF﹣ABCD=V几何体A﹣CDEF+V几何体F﹣ACB,能求出几何体EF﹣ABCD的体积.
(1)因为平面CDEF⊥平面ABCD,
平面CDEF∩平面ABCD=CD,
又四边形CDEF是正方形,
所以FC⊥CD,FC平面CDEF,
所以FC⊥平面ABCD,所以FC⊥BC.
因为△ACB是腰长为2![]() 的等腰直角三角形,
的等腰直角三角形,
所以AC⊥BC.
又AC∩CF=C,所以BC⊥平面ACF.
所以BC⊥AF.
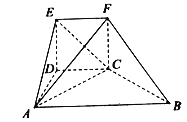
(2)因为△ABC是腰长为2![]() 的等腰直角三角形,
的等腰直角三角形,
所以AC=BC=2![]() ,AB=
,AB=![]() =4,
=4,
所以AD=BCsin∠ABC=2![]() =2,
=2,
CD=AB=BCcos∠ABC=4-2![]() cos45°=2,
cos45°=2,
∴DE=EF=CF=2,
由勾股定理得AE=![]() =2
=2![]() ,
,
因为DE⊥平面ABCD,所以DE⊥AD.
又AD⊥DC,DE∩DC=D,所以AD⊥平面CDEF.
所以V几何体EF-ABCD=V几何体A-CDEF+V几何体F-ACB
=![]()
=![]() +
+![]()
=![]()
=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=
 ,其中m>0,若存在实数b,使得关于x的方程f(x)=b有三个不同的根,则m的取值范围是 .
,其中m>0,若存在实数b,使得关于x的方程f(x)=b有三个不同的根,则m的取值范围是 . -
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,角A,B,C的对边分别为a,b,c,已知2(tanA+tanB)=
 .
.
(1)证明:a+b=2c;
(2)求cosC的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 为定义在
为定义在 上的奇函数,当
上的奇函数,当 时,函数解析式为
时,函数解析式为 .
.(Ⅰ)求
 的值,并求出
的值,并求出 在
在 上的解析式;
上的解析式;(Ⅱ)求
 在
在 上的最值.
上的最值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆M的方程为x 2+(y-2)2=1,直线l的方程为x-2y=0,点P在直线l上,过P点作圆M的切线PA,PB,切点为A,B.
(1)若∠APB=60°,试求点P的坐标;
(2)若P点的坐标为(2,1),过P作直线与圆M交于C,D两点,当
 时,求直线CD的方程;
时,求直线CD的方程;(3)求证:经过A,P,M三点的圆必过定点,并求出所有定点的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在如图所示的圆台中,AC是下底面圆O的直径,EF是上底面圆O′的直径,FB是圆台的一条母线.
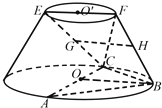
(1)已知G,H分别为EC,FB的中点,求证:GH∥平面ABC;
(2)已知EF=FB= AC=2
AC=2 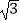 AB=BC,求二面角F﹣BC﹣A的余弦值.
AB=BC,求二面角F﹣BC﹣A的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列{an}的前n项和Sn=3n2+8n,{bn}是等差数列,且an=bn+bn+1 .
(1)求数列{bn}的通项公式;
(2)令cn=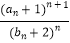 ,求数列{cn}的前n项和Tn .
,求数列{cn}的前n项和Tn .
相关试题

