【题目】某超市计划销售某种产品,先试销该产品![]() 天,对这
天,对这![]() 天日销售量进行统计,得到频率分布直方图如图.
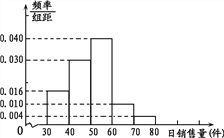
天日销售量进行统计,得到频率分布直方图如图.
(Ⅰ)若已知销售量低于50的天数为23,求![]() ;
;
(Ⅱ)厂家对该超市销售这种产品的日返利方案为:每天固定返利45元,另外每销售一件产品,返利3元;频率估计为概率.依此方案,估计日返利额的平均值.
参考答案:
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ)![]() (元)
(元)
【解析】试题分析:(Ⅰ)由频率分布直方图可知,销量低于50件的为前两组,前两组的频率为(0.016+0.030)×10=0.46,由销量低于40的天数为23可有![]() ;(Ⅱ)根据频率分布直方图计算该组数据的平均数,0.16×35+0.30×45+0.40×55+0.10×65+0.04×75=50.6,所以日平均销量为50.6件,因此估计日返利的平均值为45+50.6×3=196.8元.
;(Ⅱ)根据频率分布直方图计算该组数据的平均数,0.16×35+0.30×45+0.40×55+0.10×65+0.04×75=50.6,所以日平均销量为50.6件,因此估计日返利的平均值为45+50.6×3=196.8元.
试题解析:(Ⅰ)日销售量低于50的频率为![]() ,
,
∴![]() ,∴
,∴![]() .
.
(Ⅱ)依此方案,日返利额的平均值为
![]() (元).
(元).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图 1,在直角梯形
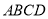 中,
中, 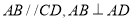 ,且
,且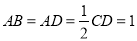 .现以
.现以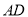 为一边向形外作正方形
为一边向形外作正方形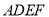 ,然后沿边
,然后沿边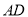 将正方形
将正方形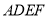 翻折,使
翻折,使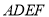 平面与平面
平面与平面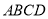 垂直,
垂直, 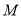 为
为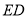 的中点,如图 2.
的中点,如图 2.(1)求证:
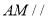 平面
平面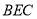 ;
;(2)求证:
 平面
平面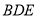 ;
;(3)求点
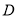 到平面
到平面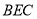 的距离.
的距离.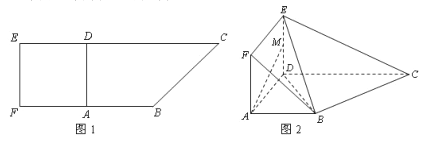
-
科目: 来源: 题型:
查看答案和解析>>【题目】公元263年左右,我国数学家刘徽发现当圆内接正多边形的边数无限增加时,多边形面积可无限逼近圆的面积,并创立了“割圆术”,利用“割圆术”刘徽得到了圆周率精确到小数点后两位的近似值
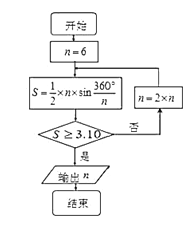
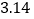 ,这就是著名的“徽率”,如图是利用刘徽的“割圆术”思想设计的一个程序框图,则输出
,这就是著名的“徽率”,如图是利用刘徽的“割圆术”思想设计的一个程序框图,则输出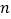 的值为 ( )
的值为 ( )(参考数据:
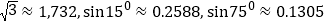 )
)
A.
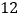 B.
B. 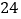 C.
C. 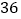 D.
D. 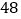
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形
 是正四棱柱
是正四棱柱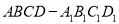 的一个截面,此截面与棱
的一个截面,此截面与棱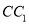 交于点
交于点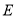 ,
, 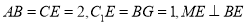 ,其中
,其中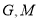 分别为棱
分别为棱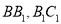 上一点.
上一点.(1)证明:平面
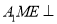 平面
平面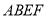 ;
;(2)
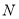 为线段
为线段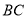 上一点,若四面体
上一点,若四面体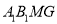 与四棱锥
与四棱锥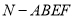 的体积相等,求
的体积相等,求 的长.
的长.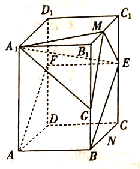
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=ln(
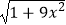 ﹣3x)+1,则f(lg2)+f(lg
﹣3x)+1,则f(lg2)+f(lg )=( )
)=( )
A.-1
B.0
C.1
D.2 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线
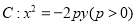 的焦点到准线的距离为
的焦点到准线的距离为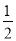 ,直线
,直线 与抛物线
与抛物线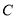 交于
交于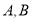 两点,过这两点分别作抛物线
两点,过这两点分别作抛物线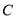 的切线,且这两条切线相交于点
的切线,且这两条切线相交于点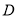 .
.(1)若
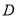 的坐标为
的坐标为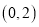 ,求
,求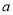 的值;
的值;(2)设线段
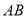 的中点为
的中点为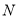 ,点
,点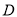 的坐标为
的坐标为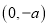 ,过
,过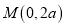 的直线
的直线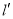 与线段
与线段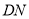 为直径的圆相切,切点为
为直径的圆相切,切点为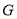 ,且直线
,且直线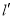 与抛物线
与抛物线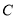 交于
交于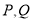 两点,证明:
两点,证明:  .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=﹣x2+ax(a∈R).
(1)当a=3时,求函数f(x)在[ ,2]上的最大值和最小值;
,2]上的最大值和最小值;
(2)当函数f(x)在( ,2)单调时,求a的取值范围.
,2)单调时,求a的取值范围.
相关试题

