【题目】我国是世界上严重缺水的国家,城市缺水尤为突出.某市为了制定合理的节水方案,从该市随机调查了100位居民,获得了他们某月的用水量,整理得到如图的频率分布直方图.
(1)求图中![]() 的值并估计样本的众数;
的值并估计样本的众数;
(2)设该市计划对居民生活用水试行阶梯水价,即每位居民用水量不超过![]() 吨的按2元/吨收费,超过
吨的按2元/吨收费,超过![]() 吨不超过2
吨不超过2![]() 吨的部分按4元/吨收费,超过2
吨的部分按4元/吨收费,超过2![]() 吨的部分按照10元/吨收费.
吨的部分按照10元/吨收费.
①用样本估计总体,为使75%以上居民在该月的用水价格不超过4元/吨,![]() 至少定为多少?
至少定为多少?
②假设同组中的每个数据用该组区间的右端点值代替,当![]() 时,估计该市居民该月的人均水费.
时,估计该市居民该月的人均水费.

参考答案:
【答案】(1)![]() ,众数为
,众数为![]() ;(2)①
;(2)①![]() ;②
;②![]() 元.
元.
【解析】
试题分析:(1)由频率分布直方图中各矩形面积总和为![]() 列出方程可求
列出方程可求![]() 的值;最高矩形的中点值即为众数;
的值;最高矩形的中点值即为众数;
(2)①由(1)可知月用水量在[0,2.5]内的频率为0.04+0.08+0.15+0.22+0.26=0.75, 区间[0,2.5]的中点值即为所求;②当![]() 时,用矩形的右端点值乘以频率再乘以相应的水费求和即可求出居民月平人均用水费.
时,用矩形的右端点值乘以频率再乘以相应的水费求和即可求出居民月平人均用水费.
试题解析:
(1)由频率分布直方图可知每段内的频率:[0,0.5]:0.04;
(0.5,1]:0.08;(1,1.5]:0. 15; (1.5,2]:0.22; (2,2.5]:0.26; (2.5,3]:0.5![]() ;(3,3.5]:0.06;
;(3,3.5]:0.06;
(3.5,4]:0.04;(4.4.5]:0.02 则由0.04+0.08+0.15+0.22+0.26+0.5![]() +0.06+0.04+0.02=1
+0.06+0.04+0.02=1
解得![]() ,
,
众数为[2,2.5]的中点值2.25
(2)①由(1)可知月用水量在[0,2.5]内的频率为0.04+0.08+0.15+0.22+0.26=0.75,
![]() 的值至少为1.25;
的值至少为1.25;
②若![]() ,
,
当居民月用水量在[0,2]时,居民该月的人均水费为:
(0.04×0.5+0.08×1+0.15×1.5+0.22×2)×2=1.53
当居民月用水量在(2,2.5]时,居民该月的人均水费为:
(2×2+0.5×4) ×0.26=1.56
当居民月用水量在(2.5,3]时,居民该月的人均水费为:
(2×2+1×4) ×0.13=1.04
当居民月用水量在(3,3.5]时,居民该月的人均水费为:
(2×2+1.5×4) ×0.06=0.6
当居民月用水量在(3.5,4]时,居民该月的人均水费为:
(2×2+2×4) ×0.04=0.489分
当居民月用水量在(4,4.5]时,居民该月的人均水费为:
(2×2+2×4+0.5×10) ×0.02=0.3410分
![]() 居民月人均水费为1.53+1.56+1.04+0. 6+0.48+0.34=5.55元.1
居民月人均水费为1.53+1.56+1.04+0. 6+0.48+0.34=5.55元.1
-
科目: 来源: 题型:
查看答案和解析>>【题目】某农科所对冬季昼夜温差大小与某反季节大豆新品种发芽多少之间的关系进行分析研究,他们分别记录了12月1日至12月5日的每天昼夜温差与实验室每天每100颗种子中的发芽数,得到如下资料:
日 期
12月1日
12月2日
12月3日
12月4日
12月5日
温差x(°C)
10
11
13
12
8
发芽数y(颗)
23
25
30
26
16
(1)请根据12月2日至12月4日的数据,求出y关于x的线性回归方程
 (其中已计算出
(其中已计算出 );
);(2)若由线性回归方程得到的估计数据与所选出的检验数据(选取的检验数据是12月1日与12月5日的两组数据)的误差均不超过2颗,则认为得到的线性回归方程是可靠的,试问(2)中所得的线性回归方程是否可靠?
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1-i)2·i等于
A.2-2iB. 2+2iC.-2 D.2
-
科目: 来源: 题型:
查看答案和解析>>【题目】某单位最近组织了一次健身活动,活动分为登山组和游泳组,且每个职工至多参加其中一组.在参加活动的职工中,青年人占42.5%,中年人占47.5%,老年人占10%.登山组的职工占参加活动总人数的
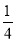 ,且该组中青年人占50%,中年人占40%,老年人占10%.为了了解各组不同年龄层次的职工对本次活动的满意程度,现用分层抽样的方法从参加活动的全体职工中抽取一个容量为200的样本.试确定:
,且该组中青年人占50%,中年人占40%,老年人占10%.为了了解各组不同年龄层次的职工对本次活动的满意程度,现用分层抽样的方法从参加活动的全体职工中抽取一个容量为200的样本.试确定:(1)游泳组中,青年人、中年人、老年人分别所占的比例;
(2)游泳组中,青年人、中年人、老年人分别应抽取的人数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下面是一段演绎推理:
大前提:如果直线平行于平面,则这条直线平行于平面内的所有直线;
小前提:已知直线b∥平面α,直线a平面α;
结论:所以直线b∥直线a.在这个推理中( )
A. 大前提正确,结论错误 B. 大前提错误,结论错误
C. 大、小前提正确,只有结论错误 D. 小前提与结论都是错误的
-
科目: 来源: 题型:
查看答案和解析>>【题目】若f(x)为R上的奇函数,且1是该函数的一个零点,则f(0)+f(-1)=________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某高校在2012年的自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩分组,得到的频率分布表如图所示.
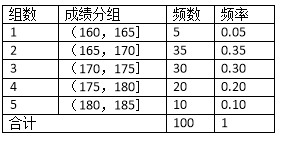
(1)为了能选拔出最优秀的学生,该高校决定在笔试成绩高的第3、4、5组中用分层抽样抽取6名学生进入第二轮面试,求第3、4、5组每组各抽取多少名学生进入第二轮面试?
(2)在(1)的前提下,学校决定在6名学生中随机抽取2名学生接受A考官的面试,求第四组至少有一名学生被考官A面试的概率?
相关试题

