【题目】已知函数![]() 的图像与直线
的图像与直线![]() 相切.
相切.
(Ⅰ)求![]() 的值,并求
的值,并求![]() 的单调区间;
的单调区间;
(Ⅱ)若![]() ,设
,设![]() ,讨论函数
,讨论函数![]() 的零点个数.
的零点个数.
参考答案:
【答案】(Ⅰ) ![]() ,函数的单调减区间为
,函数的单调减区间为![]() ,增区间为
,增区间为![]() ; (Ⅱ)答案见解析.
; (Ⅱ)答案见解析.
【解析】试题分析:
(Ⅰ)由题意结合导函数与原函数切线的关系得到关于实数m的方程,解方程可得m=1,则函数的单调减区间为![]() ,增区间为
,增区间为![]() ;
;
(Ⅱ)原问题转化为函数![]() 的图象的交点个数,分类讨论可得:
的图象的交点个数,分类讨论可得:
当![]() 时,函数
时,函数![]() 无零点;
无零点;
当![]() 或
或![]() 时,函数
时,函数![]() 恰有一个零点;
恰有一个零点;
当![]() 时,函数
时,函数![]() 恰有两个零点.
恰有两个零点.
试题解析:
(I)设![]() 的图像与直线
的图像与直线![]() 相切于点
相切于点![]() ,
,
![]() ,
, ![]()
则 即
即
解得:![]()
由![]() 得
得![]() ;
;![]() 得
得![]() ;
;
所以函数![]() 的单调减区间为
的单调减区间为![]() ;增区间为
;增区间为![]()
(II)![]()
![]()
![]() ;
;
![]()
记函数![]()
![]()
由![]() 得
得![]() ;
;![]() 得
得![]()
![]() 在
在![]() 上单调递增;在
上单调递增;在![]() 上单调递减
上单调递减
![]()
又![]() 时,
时,![]() ;
;
![]() 时,
时,![]() ;且
;且![]() .
.
则:当![]() 时,
时, ![]() 与
与![]() 的图像无交点,函数
的图像无交点,函数![]() 无零点;
无零点;
当![]() 或
或![]() 时,
时, ![]() 与
与![]() 的图像恰有一个交点,函数
的图像恰有一个交点,函数![]() 恰有一个零点;
恰有一个零点;
当![]() 时,
时, ![]() 与
与![]() 的图像恰有两个交点,函数
的图像恰有两个交点,函数![]() 恰有两个零点.
恰有两个零点.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在正方体ABCD﹣A1B1C1D1中,E为DD1的中点,则下列直线中与平面ACE平行的是( )
A.BA1
B.BD1
C.BC1
D.BB1 -
科目: 来源: 题型:
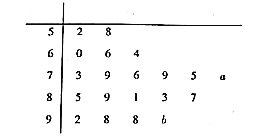
查看答案和解析>>【题目】某班20名同学某次数学测试的成绩可绘制成如下茎叶图,由于其中部分数据缺失,故打算根据茎叶图中的数据估计全班同学的平均成绩.
(1)完成频率分布直方图;
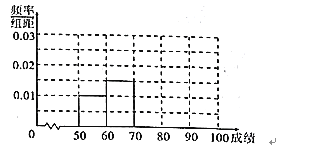
(2)根据(1)中的频率分布直方图估计全班同学的平均成绩
 (同一组中的数据用该组区间的中点值作代表);
(同一组中的数据用该组区间的中点值作代表);(3)设根据茎叶图计算出的全班的平均成绩为
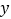 ,并假设
,并假设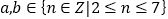 ,且
,且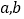 各自取得每一个可能值的机会相等,在(2)的条件下,求概率
各自取得每一个可能值的机会相等,在(2)的条件下,求概率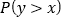 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在长方体ABCD﹣A1B1C1D1中,E是CD上一点,AB=AD=3,AA1=2,CE=1,P是AA1上一点,且DP∥平面AEB1 , F是棱DD1与平面BEP的交点,则DF的长为( )
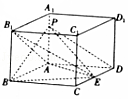
A.1
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,边长为3的正方形
 所在平面与等腰直角三角形
所在平面与等腰直角三角形 所在平面互相垂直,
所在平面互相垂直,  ,且
,且 ,
,  .
.(Ⅰ)求证:
 平面
平面 ;
;(Ⅱ)求二面角
 的余弦值.
的余弦值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若0<x<
 ,则2x与3sin x的大小关系( )
,则2x与3sin x的大小关系( )
A.2x>3sin x
B.2x<3sin x
C.2x=3sin x
D.与x的取值有关 -
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC的内角A,B,C的对边分别为a,b,c,已知△ABC的面积为
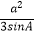 .
.
(1)求sinBsinC;
(2)若6cosBcosC=1,a=3,求△ABC的周长.
相关试题

