【题目】已知数列![]() 中,
中,![]() ,且点
,且点![]() 在直线
在直线![]() 上.
上.
⑴求数列![]() 的通项公式;
的通项公式;
⑵若函数![]() (
(![]() ,且
,且![]() ),求函数
),求函数![]() 的最小值;
的最小值;
⑶设![]() ,
,![]() 表示数列
表示数列![]() 的前
的前![]() 项和,试问:是否存在关于
项和,试问:是否存在关于![]() 的整式
的整式![]() ,使得
,使得![]() 对于一切不小于2的自然数
对于一切不小于2的自然数![]() 恒成立?若存在,写出
恒成立?若存在,写出![]() 的解析式,并加以证明;若不存在,试说明理由.
的解析式,并加以证明;若不存在,试说明理由.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() ,证明见解析.
,证明见解析.
【解析】
试题分析:(1)将点![]() 代入直线
代入直线![]() 得到
得到![]() ,
,![]() 数列
数列![]() 是以
是以![]() 为首项,
为首项,![]() 为公差的等差数列,再由
为公差的等差数列,再由![]() 得到
得到![]() 的通项公式;(2)由(1)可得
的通项公式;(2)由(1)可得![]() ,
,
![]()
![]() ,
,![]() ,
,![]() 是单调递增的,故
是单调递增的,故![]() 的最小值是
的最小值是![]() ;(3)由(1)及
;(3)由(1)及![]() ,
,![]() ,即
,即![]() ,
,![]() ,
,![]()
![]() ,最后将该式整理即可得出
,最后将该式整理即可得出![]() .
.
试题解析:⑴![]() 点
点![]() 在直线
在直线![]() 上,即
上,即![]() ,且
,且![]() ,
,
![]() 数列
数列![]() 是以
是以![]() 为首项,
为首项,![]() 为公差的等差数列,
为公差的等差数列,
![]() ,
,![]() 也满足,
也满足,![]()
⑵![]()
![]() ,
,
![]()
![]() ,
,
![]() ,
,
![]() 是单调递增的,故
是单调递增的,故![]() 的最小值是
的最小值是![]() .
.
⑶![]()
![]() ,
,![]() ,
,
即![]() ,
,![]() ,
,
![]()
![]() ,
,![]() .
.
故存在关于![]() 的整式
的整式![]() ,使等式对于一切不小于
,使等式对于一切不小于![]() 的自然数
的自然数![]() 恒成立.
恒成立.
法二:先由![]() 的情况,猜想出
的情况,猜想出![]() ,再用数学归纳法证明.
,再用数学归纳法证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为考察某种药物预防禽流感的效果,进行动物家禽试验,调查了100个样本,统计结果为:服用药的共有60个样本,服用药但患病的仍有20个样本,没有服用药且未患病的有20个样本.
(1)根据所给样本数据完成下面2×2列联表;
(2)请问能有多大把握认为药物有效?
不得禽流感
得禽流感
总计
服药
不服药
总计
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,正方体ABCD-A1B1C1D1中,E,F分别是AB,AA1的中点.
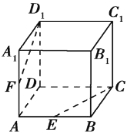
求证:(1)E,C,D1,F四点共面;
(2)CE,D1F,DA三线共点.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,某班一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的污损,其中,频率分布直方图的分组区间分别为
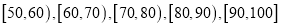 ,据此解答如下问题.
,据此解答如下问题.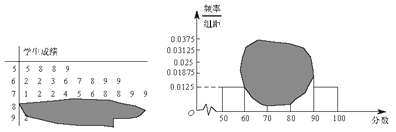
(Ⅰ)求全班人数及分数在
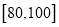 之间的频率;
之间的频率;(Ⅱ)现从分数在
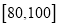 之间的试卷中任取 3 份分析学生情况,设抽取的试卷分数在
之间的试卷中任取 3 份分析学生情况,设抽取的试卷分数在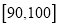 的份数为
的份数为 ,求
,求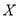 的分布列和数学望期.
的分布列和数学望期. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
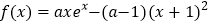 (其中
(其中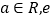 为自然对数的底数,
为自然对数的底数,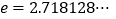 ).
).(1)若
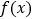 仅有一个极值点,求
仅有一个极值点,求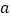 的取值范围;
的取值范围;(2)证明:当
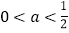 时,
时,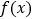 有两个零点
有两个零点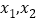 ,且
,且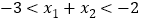 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】设集合A={x|-2≤x≤5},B={x|m+1≤x≤2m-1}.
(1)若BA,求实数m的取值范围;
(2)当x∈R时,不存在元素x使x∈A与x∈B同时成立,求实数m的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设函数f(x)=|2x-1|+|2x-a|+a,x∈R.
(1)当a=3时,求不等式f(x)>7的解集;
(2)对任意x∈R恒有f(x)≥3,求实数a的取值范围.
相关试题

