【题目】已知函数f(x)=![]() .(a>0)
.(a>0)
(1)若a=1,证明:y=f(x)在R上单调递减;
(2)当a>1时,讨论f(x)零点的个数.
参考答案:
【答案】见解析
【解析】(1)证明:当x≥1时,f′(x)=![]() -1≤0,f(x)在[1,+∞)上单调递减,f(x)≤f(1)=0;
-1≤0,f(x)在[1,+∞)上单调递减,f(x)≤f(1)=0;
当x<1时,f′(x)=ex-1-1<0,f(x)在(-∞,1)上单调递减,且此时f(x)>0.
所以y=f(x)在R上单调递减.
(2)若x≥a,则f′(x)=![]() -a≤
-a≤![]() -a<0(a>1),
-a<0(a>1),
所以此时f(x)单调递减,令g(a)=f(a)=ln a-a2+1,
则g′(a)=![]() -2a<0,所以f(a)=g(a)<g(1)=0,
-2a<0,所以f(a)=g(a)<g(1)=0,
即f(x)≤f(a)<0,故f(x)在[a,+∞)上无零点.
当x<a时,f′(x)=ex-1+a-2,
①当a>2时,f′(x)>0,f(x)单调递增,
又f(0)=e-1>0,f![]() <0,所以此时f(x)在
<0,所以此时f(x)在![]() 上有一个零点.
上有一个零点.
②当a=2时,f(x)=ex-1,此时f(x)在(-∞,2)上没有零点.
③当1<a<2时,令f′(x0)=0,解得x0=ln(2-a)+1<1<a,所以f(x)在(-∞,x0)上单调递减,在(x0,a)上单调递增.
f(x0)=e![]() +(a-2)x0=e
+(a-2)x0=e![]() (1-x0)>0,
(1-x0)>0,
所以此时f(x)没有零点.
综上,当1<a≤2时,f(x)没有零点;当a>2时,f(x)有一个零点.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为创建全国文明城市,某区向各事业行政单位征集“文明过马路”义务督导员.从符合条件的600名志愿者中随机抽取100名,按年龄作分组如下:
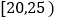 ,
,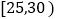 ,
,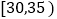 ,
,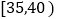 ,
,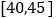 ,并得到如下频率分布直方图.
,并得到如下频率分布直方图.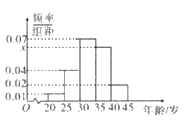
(I)求图中
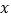 的值,并根据频率分布直方图统计这600名志愿者中年龄在
的值,并根据频率分布直方图统计这600名志愿者中年龄在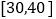 的人数;
的人数;(II)在抽取的100名志愿者中按年龄分层抽取5名参加区电视台“文明伴你行”节目录制,再从这5名志愿者中随机抽取2名到现场分享劝导制止行人闯红灯的经历,求至少有1名年龄不低于35岁的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】盐化某厂决定采用以下方式对某块盐池进行开采:每天开采的量比上一天减少
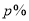 ,10天后总量变为原来的一半,为了维持生态平衡,剩余总量至少要保留原来的
,10天后总量变为原来的一半,为了维持生态平衡,剩余总量至少要保留原来的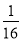 ,已知到今天为止,剩余的总量是原来的
,已知到今天为止,剩余的总量是原来的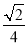 .
.(1)求
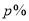 的值;
的值;(2)到今天为止,工厂已经开采了几天?
(3)今后最多还能再开采多少天?
-
科目: 来源: 题型:
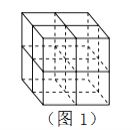
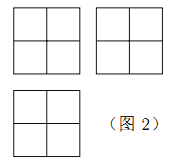
查看答案和解析>>【题目】张师傅想要一个如图1所示的钢筋支架的组合体,来到一家钢制品加工店定制,拿出自己画的组合体三视图(如图2所示).店老板看了三视图,报了最低价,张师傅觉得很便宜,当即甩下定金和三视图,约定第二天提货.第二天提货时,店老板一脸坏笑的捧出如图3–1所示的组合体,张师傅一看,脸都绿了:“奸商,怎能如此偷工减料”.店老板说,我是按你的三视图做的,要不我给你加一个正方体,但要加价,随机加上了一个正方体,得到如图3–2所示的组合体;张师傅脸还是绿的,店老板又加上一个正方体,组成了如图 3–3 所示的组合体,又加价;张师傅脸继续绿,店老板再加一个正方体,组成如图 3–4 所示的组合体,再次加价;双方就三视图争吵不休……
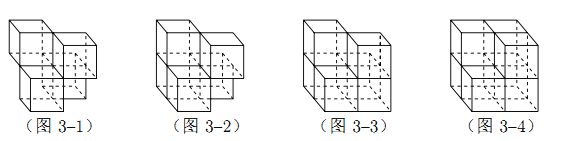
你认为店老板提供的
 个组合体的三视图与张师傅画的三视图一致的个数是( )
个组合体的三视图与张师傅画的三视图一致的个数是( )A.
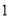 B.
B. 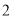 C.
C.  D.
D. 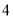
-
科目: 来源: 题型:
查看答案和解析>>【题目】某地政府鉴于某种日常食品价格增长过快,欲将这种食品价格控制在适当范围内,决定对这种食品生产厂家提供政府补贴,设这种食品的市场价格为x元/千克,政府补贴为t元/千克,根据市场调查,当16≤x≤24时,这种食品市场日供应量p万千克与市场日需求量q万千克近似地满足关系:p=2(x+4t-14)(x≥16,t≥0),q=24+8ln
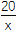 (16≤x≤24).当p=q时的市场价格称为市场平衡价格.
(16≤x≤24).当p=q时的市场价格称为市场平衡价格.(1)将政府补贴表示为市场平衡价格的函数,并求出函数的值域.
(2)为使市场平衡价格不高于每千克20元,政府补贴至少为每千克多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
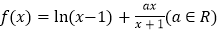 .
.(Ⅰ)若函数
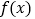 在区间
在区间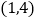 上单调递增,求
上单调递增,求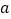 的取值范围;
的取值范围;(Ⅱ)若函数
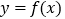 的图象与直线
的图象与直线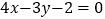 相切,求
相切,求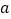 的值.
的值.
相关试题

